Table of Contents
1. What’s this about?
Signed distance function (SDF) seems to be a commonly used math tool in computer graphics. I first came across the SDF concept in one of Inigo Quilez‘s Youtube tutorials, where he talked about the derivation of SDF to a line segment.
This post will talk about SDF to oriented 2D boxes. I will start from the simple case where the boxes are centered at the origin, without any rotations. If you prefer video format, you could check out Inigo’s The SDF of A Box tutorial. In fact, much of the derivations about this part are adopted from his video (due credits to him).
Then I will move onto the general case where the boxes have arbitrary locations and orientations. Again, Inigo has this covered in his written tutorials. The code snippets in that page are in Java(?), and can be executed with real-time feedback in Shadertoy (see links in that page). In this post, I will show codes in Python, and plots created using matplotlib. So not as eye-candy as the Shadertoy graphics, but the point is to understand the SDF function, not about the visual.
After that, I will show a variant of the SDF-to-oriented-boxes that I crafted, with slightly different distance definitions. Perhaps it has been created before, with a proper name. For now, I will call it SDF-L1, for its usage of the L1-norm as distance metric, instead of the Euclidean (L2) distance. This turns out to be useful in computing the approximated Intersection-Over-Union (IoU) between pairs of oriented 2D boxes. I will get to that in a later post.
2. SDF to oriented 2D boxes, simple case
2.1. Formulate the problem
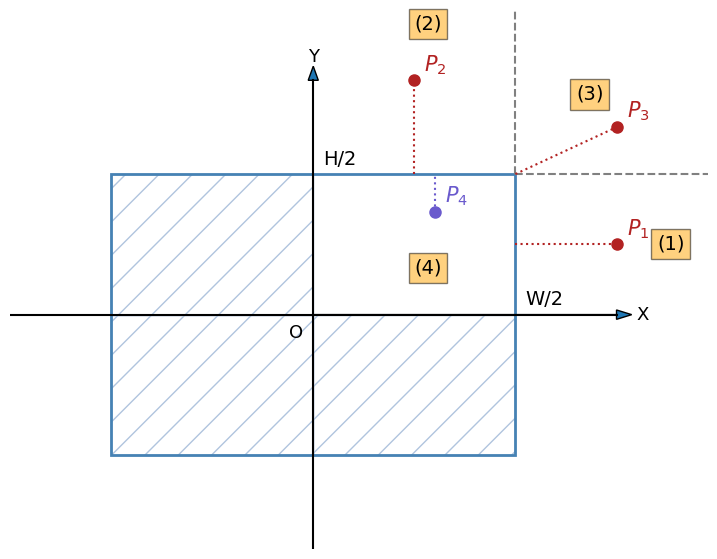

Figure 1: A box with width \(W\) and height \(H\), centered at the origin \(O\). The 2nd – 4th quadrants are shaded, and SDF values in these areas can be covered by symmetrical relationship with the 1st quadrant. The 1st qudrant is divided into 3 regions, labeled (1), (2) and (3), each with a representative point \(P_1\), \(P_2\) and \(P_3\). The interior region of the 1st quadrant is labeled (4).
Let’s start from the simple case: a box that:
- centers at the origin
- with no rotation
- has width \(W\) and height \(H\)
See Figure 1 for a schematic.
Because of the left-right symmetry about the y-axis, everything on the left half (\(x < 0\)) can be mirrored into the right half (\(x >= 0\)). Similarly for the top-down symmetry. Therefore, we only need to deal with the 1st quadrant, where \(x >= 0,\, y >= 0\). This mirroring can be easily achieved by taking the absolute value of the x- and y- coordinates of the point \(P\):
\begin{equation} |P|=(|P_x|, |P_y|) \end{equation}The SDF of a point \(P\) outside of the box to the box is the shortest Euclidean distance between \(P\) and any point along the edges of the box, there are 3 possible scenarios, dividing the 1st quadrant into 3 regions, labeled (1), (2) and (3) in Figure 1.
When \(P\) falls inside the box, the SDF is still the shortest distance between \(P\) and the edges of the box. This region is labeled as (4).
And we also take the convention that points outside of the box have positive SDFs, those inside have negative SDFs.
To summarize, we need to deal with the following 4 scenarios:
- Region 1: \(|P_x| >= W/2\), \(|P_y| < H/2\), where \((P_x, P_y)\) is the coordinate of point \(P\).
- Region 2: \(|P_x| < W/2\), \(|P_y| >= H/2\).
- Region 3: \(|P_x| >= W/2\), \(|P_y| >= H/2\).
- Region 4: \(|P_x| < W/2\), \(|P_y| < H/2\).
2.2. For a point outside of the box
Now examine the first 3 cases. The SDF for \(P_1\), \(P_2\) and \(P_3\) are respectively:
- Region 1: \(SDF(P, box) = |P_x| – W/2\).
- Region 2: \(SDF(P, box) = |P_y| – H/2\).
- Region 3: \(SDF(P, box) = ||P| – (W/2, H/2)|_2 = \sqrt{(|P_x| – W/2)^2 + (|P_y| – H/2)^2}\).
where \(||P| – (W/2, H/2)|_2\) is the Euclidean distance (L2-norm) of the vector linking the 2 points: \(P\) and \((W/2, H/2)\).
It turns out that the above 3 expressions can by combined into a unified one:
\begin{equation} \label{orgc2d1066} SDF(P, box) = |\max(|P| – (W/2, H/2), 0)|_2 \end{equation}To see how this works, take for instance the Region 1 case. Because \(|P_x| >= W/2\), \(|P_y| < H/2\), \(\max(|P| - (W/2, H/2), 0) = (|P_x| - W/2, 0)\). Then the length of \((|P_x| - W/2, 0)\) is just \(|P_x| - W/2\), indeed the Region 1 SDF shown above.
You could verify that this also holds for Region 2 and Region 3.
The reason for doing this unification rather than using if-else branches is that the code will be able to run more efficiently doing streamlined executions, rather than if-else control flows.
2.3. For a point inside the box
Now for Region 4, because \(P\) is inside the box, the SDF is either the x- distance to the box’s right edge (\(|P_x| – W/2\)), or the y- distance to the box’s top edge (\(|P_y| – H/2\)), whichever has the smaller absolute value (note that both are negative numbers).
We use \(\max_c(Q)\) to denote the maximum component of the point \(Q\): \(\max_c(Q) \equiv \max(Q_x, Q_y)\). Then the SDF of a point inside the box is:
\begin{equation} \label{org7e3630f} SDF(P, box) = \max_c(|P| – (W/2, H/2)) \end{equation}Since we know both of the x- and y- components are negative, the maximum of them corresponds to the one with the smaller absolute value, thereby closer to the box edge.
2.4. Combine them all
Notice that for all of the 4 scenarios, we need to compute a term \(|P| – (W/2, H/2)\), which is the vector linking \(P\) and the box corner. Let’s give it a separate label:
\begin{equation} \label{org0856bb0} Q = |P| – (W/2, H/2) \end{equation}Substituting it into Equation \eqref{orgc2d1066} gives the expression for SDF outside of the box:
\begin{equation} \label{org798bd52} SDF(P, box) = |\max(Q, 0)|_2, \; \text{P is outside} \end{equation}Substituting it into Equation \eqref{org7e3630f} gives the expression for SDF inside the box:
\begin{equation} \label{org3854c8f} SDF(P, box) = \max_c(Q), \; \text{P is inside} \end{equation}These 2 cases can be merged into one:
\begin{equation} \label{org7ec38a5} SDF(P, box) = |\max(Q, 0)|_2 + \min(\max_c(Q), 0) \end{equation}It’s interesting to see how compact the final expression is.
2.5. Summary
A quick summary of what we have got:
- The box has width \(W\) and height \(H\), centered at the origin, with no rotation.
- The SDF of an arbitrary point \(P\) is defined as the shortest distance between \(P\) and the box edge.
- Symmetries about the x- and y- axes allow us to deal with only the 1st quadrant. To achieve this, we take the absolute values of \(P\): \(|P|\).
- Compute an intermediate term \(Q = |P| – (W/2, H/2)\).
- When \(P\) is outside of the box, SDF is positive, and is given as \(|max(Q, 0)|_2\), where \(|\cdot|_2\) is the Euclidean distance (L2-norm).
- When \(P\) is inside the box, SDF is negative, and is given as \(\max_c(Q)\), where \(\max_c(Q)\) takes the maximum component of vector \(Q\).
- Lastly, the above 2 expressions can be combined into \(SDF(P, box) = |\max(Q, 0)|_2 + \min(\max_c(Q), 0)\), covering both outside and inside cases.
2.6. Python implementation
I’m using numpy as the only dependency. The code is given below:
import numpy as np def sdf_box(p, box_w, box_h, interior_neg=True): '''Signed distance to box centered at origin Args: p (ndarray): (n, 2) array, (x, y) coordinates of points to compute SDF. box_w (float): total width of box. box_h (float): total height of box. Keyword Args: interior_neg (bool): if True, SDF inside boxes take negative values. Returns: res (1darray): 1d array with length <n>, signed distances to box. ''' p = np.atleast_2d(p) box_wh = np.array([box_w, box_h]) / 2 qq = np.abs(p) - box_wh[None, :] outer = np.linalg.norm(np.maximum(qq, 0), axis=1) inner = np.minimum(np.max(qq, axis=1), 0.) if not interior_neg: inner = np.abs(inner) res = outer + inner return res
A couple of points to note:
- The points to compute the SDFs are given in
p, and is anndarraywith shape(n, 2). - I added a
interior_negkeyword argument. If set toTrue, the SDFs inside the box have negative values, as explained above. When set toFalse, those negative values are inverted by taking theabs().
To see the difference created by interior_neg, here is a simple
example:
import matplotlib.pyplot as plt from matplotlib.patches import Rectangle def plot_imshow(var, ax, x, y): vmax = abs(var).max() vmin = -vmax cs = ax.contourf(x, y, var, levels=16, cmap=plt.cm.RdBu_r, vmax=vmax, vmin=vmin) plt.colorbar(cs, ax=ax, orientation='horizontal') return x = np.linspace(-4, 4, 200) y = np.linspace(-3, 3, 100) xx, yy = np.meshgrid(x, y) points = np.c_[xx.flatten(), yy.flatten()] # ---------------SDF to centered h-box--------------- w, h = 4, 3 dists1 = sdf_box(points, w, h, True) dists1 = dists1.reshape(len(y), len(x)) dists2 = sdf_box(points, w, h, False) dists2 = dists2.reshape(len(y), len(x)) # plot fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(10, 5)) ax = axes[0] rect = Rectangle((-w/2, -h/2), w, h, edgecolor='k', fill=False, lw=1) plot_imshow(dists1, ax, x, y) ax.add_patch(rect) ax.set_aspect(1) ax.set_title('(a) interior_neg=True') ax = axes[1] rect = Rectangle((-w/2, -h/2), w, h, edgecolor='k', fill=False, lw=1) plot_imshow(dists2, ax, x, y) ax.add_patch(rect) ax.set_aspect(1) ax.set_title('(b) interior_neg=False') fig.show()
Here is the output figure:
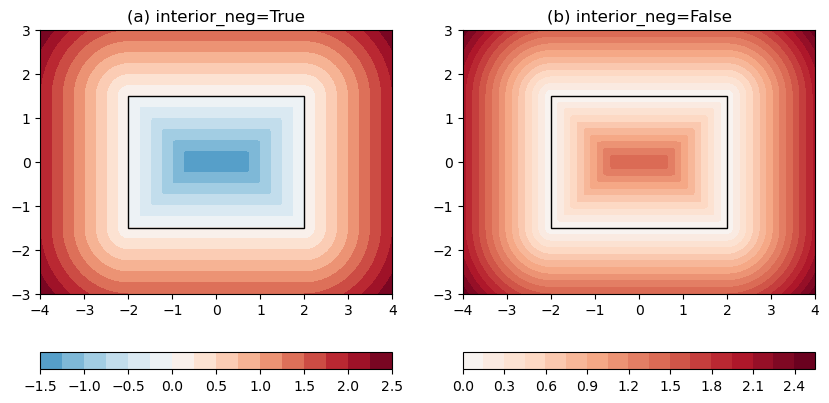

Figure 2: SDF to a box centered at origin with no rotation. (a) SDFs inside the box take negative values. (b) SDFs inside the box take positive values. The box itself is drawn as black.
3. SDF to oriented 2D boxes, general case
3.1. The solution
Moving onto the general case where the box takes arbitrary location with arbitrary orientation.
Firstly, denote the box center coordinate as \(C = (C_x, C_y)\), and the box rotation as \(\theta\), where \(\theta\) is the angle formed between the box’s width edge and the x- axis.
To generalize from our above shown simple case, all we need to do:
- Translate the query point \(P\) by \(-C\) so the box is centered,
- Rotate the query point by \(-\theta\) so the box is no longer oriented,
- Compute the SDF using the above simple case formula.
3.2. Python implementation
As it is relatively straightforward to re-formulate the problem to our known simple case solution, I’ll jump to Python implementation. Code below:
def sdf_obox(p, xc, yc, w, h, angle, interior_neg=True): '''Signed distance to oriented box at any location Args: p (ndarray): (n, 2) array, (x, y) coordinates of points to compute SDF. xc (float): x-center location of box. yc (float): y-center location of box. w (float): total width of box. h (float): total height of box. angle (float): orientation angle, in radian. Keyword Args: interior_neg (bool): if True, SDF inside boxes take negative values. Returns: res (1darray): 1d array with length <n>, signed distances to box. ''' rot = np.array([[np.cos(angle), -np.sin(angle)], [np.sin(angle), np.cos(angle)]]) center = np.array([xc, yc]) p = np.atleast_2d(p) dp = p - center[None, :] dp = dp.dot(rot) # NOTE: right-multiplication to rotate -angle return sdf_box(dp, w, h, interior_neg)
A few points to note:
- The target box is encoded by its center location (
xc,yc), its sizes (w,h) and orientation (angle, in radian). The rotation matrix is
\begin{equation} R = \begin{bmatrix} \cos \theta & -\sin \theta \\\sin \theta & \cos \theta \end{bmatrix} \end{equation}Note that to rotate by \(-\theta\), we use right-multiplication (\([P_x, P_y] \cdot R\)). The left-multiplication would rotate it by \(\theta\).
- After the translation and rotation, we simply call the previously
shown
sdf_box()function to the get the result. - Again,
interior_negcontrols whether interior SDFs have negative values or not.
A simple example:
xc, yc, w, h, angle = 1, 0.5, 4, 3, np.pi/6 rot = np.array([[np.cos(angle), -np.sin(angle)], [np.sin(angle), np.cos(angle)]]) dists1 = sdf_obox(points, xc, yc, w, h, angle, True) dists1 = dists1.reshape(len(y), len(x)) dists2 = sdf_obox(points, xc, yc, w, h, angle, False) dists2 = dists2.reshape(len(y), len(x)) fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(10, 5)) ax = axes[0] bl_x, bl_y = rot.dot(np.array([-w/2, -h/2])) rect = Rectangle((bl_x+xc, bl_y+yc), w, h, angle=angle/np.pi*180, edgecolor='k', fill=False, lw=1) plot_imshow(dists1, ax, x, y) ax.add_patch(rect) ax.set_aspect(1) ax.set_title('(a) interior_neg=True') ax = axes[1] rect = Rectangle((bl_x+xc, bl_y+yc), w, h, angle=angle/np.pi*180, edgecolor='k', fill=False, lw=1) plot_imshow(dists2, ax, x, y) ax.add_patch(rect) ax.set_aspect(1) ax.set_title('(b) interior_neg=False') fig.show()
Here is the output figure:
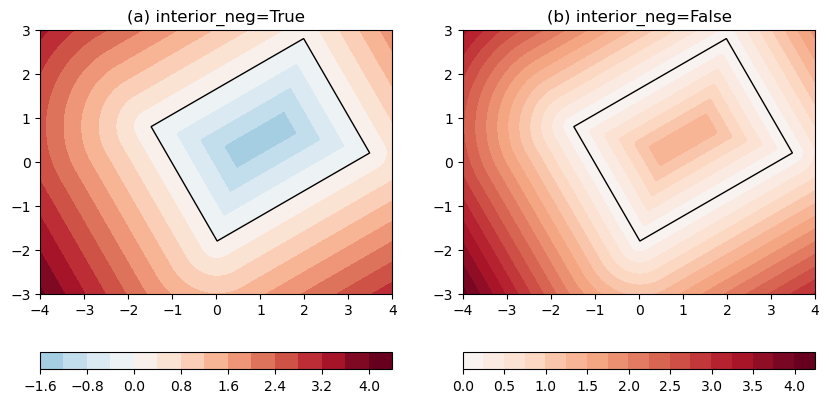

Figure 3: SDF to a box centered at (1, 0.5) with 30 degree rotation. (a) SDFs inside the box take negative values. (b) SDFs inside the box take positive values. The box itself is drawn as black.
4. SDF-L1: SDF to oriented 2D boxes, with L1-norm distance
4.1. New definition with L1 distance measure
Based on the formulation above, I then crafted a slightly different type of SDF-to-oriented-2D-boxes. Figure 4 below shows a schematic to this new definition.
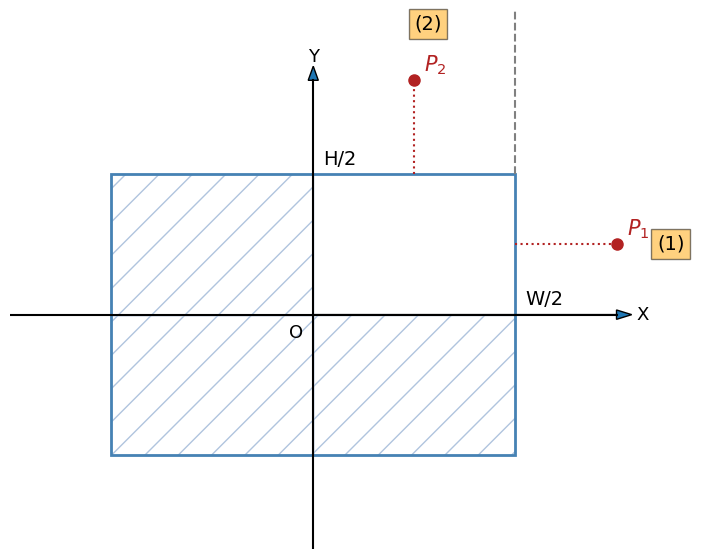

Figure 4: A box with width \(W\) and height \(H\), centered at the origin \(O\). The 1st qudrant is divided into 2 regions, labeled (1) and (2).
There are 2 main differences from the conventional SDF definition:
- Only defined for points outside of the box,
- The 1st quadrant is divided into only 2 regions:
- Region 1: \(|P_x| >= W/2\), and the SDF is \(SDF(P, box) = |P_x| – W/2\).
- Region 2: \(|P_x| < W/2\), and the SDF is \(SDF(P, box) = |P_y| - H/2\).
Note that there is no dedicated Region 3 for points located into the diagonal corner region, therefore the SDF computation never uses L2-norm, therefore I call it SDF-L1, for SDF with L1-norm distance. However, as will be shown below, I also add negative signs to points to the left/bottom side of the box (for reasons that I will explain in a later post), it is not strictly L1-norm. So it is a temporary name. If you have a better idea please let me know in the comment down below.
4.2. Python implementation
This new function can be easily worked out by modifying the existing code shown above. Here is the function for boxes centered at origin and without rotation:
def sdf_box_l1(p, box_w, box_h, return_comps=False): '''L1-signed distance to box centered at origin Args: p (ndarray): (n, 2) array, (x, y) coordinates of points to compute SDF. box_w (float): total width of box. box_h (float): total height of box. Keyword Args: return_comps (bool): if True, also return the x- and y- distance components. Returns: res (1darray): 1d array with length <n>, signed distances to box with l1-distance. comps (ndarray): (n, 2) array, the x- and y- distance components. ''' p = np.atleast_2d(p) box_wh = np.array([box_w, box_h]) / 2 qq = np.abs(p) - box_wh[None, :] dx, dy = qq[:, 0], qq[:, 1] sign = dx > 0 # distances to left- and right- edges: x_comp = np.maximum(dx, 0) * sign * np.sign(p[:, 0]) # distances to top- and bottom- edges: y_comp = np.maximum(dy, 0) * (1 - sign) * np.sign(p[:, 1]) res = x_comp + y_comp if return_comps: return res, np.c_[x_comp, y_comp] else: return res
And this one handles the general case with arbitrary box location and orientation:
def sdf_obox_l1(p, xc, yc, w, h, angle, return_comps=False): '''L1-signed distance to oriented box at any location Args: p (ndarray): (n, 2) array, (x, y) coordinates of points to compute SDF. xc (float): x-center location of box. yc (float): y-center location of box. w (float): total width of box. h (float): total height of box. angle (float): orientation angle, in radian. Keyword Args: return_comps (bool): if True, also return the x- and y- distance components. Returns: res (1darray): 1d array with length <n>, signed distances to box with l1-distance. comps (ndarray): (n, 2) array, the x- and y- distance components. ''' rot = np.array([[np.cos(angle), -np.sin(angle)], [np.sin(angle), np.cos(angle)]]) center = np.array([xc, yc]) p = np.atleast_2d(p) dp = p - center[None, :] dp = dp.dot(rot) # NOTE: right-multiplication to rotate -angle return sdf_box_l1(dp, w, h, return_comps)
To see how this new SDF differs from the conventional one, here is a simple example:
xc, yc, w, h, angle = 1, 0.5, 4, 3, np.pi/6 rot = np.array([[np.cos(angle), -np.sin(angle)], [np.sin(angle), np.cos(angle)]]) dists1 = sdf_obox(points, xc, yc, w, h, angle, True) dists1 = dists1.reshape(len(y), len(x)) dists2 = sdf_obox_l1(points, xc, yc, w, h, angle, False) dists2 = dists2.reshape(len(y), len(x)) fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(10, 5)) ax = axes[0] bl_x, bl_y = rot.dot(np.array([-w/2, -h/2])) rect = Rectangle((bl_x+xc, bl_y+yc), w, h, angle=angle/np.pi*180, edgecolor='k', fill=False, lw=1) plot_imshow(dists1, ax, x, y) ax.add_patch(rect) ax.set_aspect(1) ax.set_title('(a) Normal SDF') ax = axes[1] rect = Rectangle((bl_x+xc, bl_y+yc), w, h, angle=angle/np.pi*180, edgecolor='k', fill=False, lw=1) plot_imshow(dists2, ax, x, y) ax.add_patch(rect) ax.set_aspect(1) ax.set_title('(b) SDF with L1 distance') fig.show()
Here is the output figure:
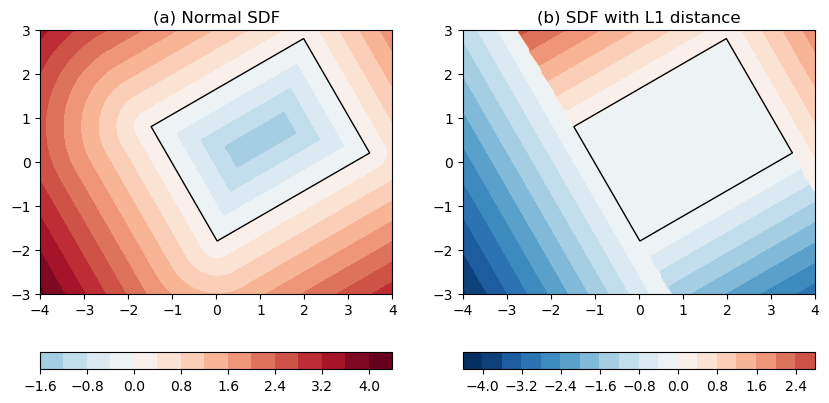

Figure 5: SDF to a box centered at (1, 0.5) with 30 degree rotation. (a) normal SDFs. (b) SDFs with L1-norm distance. The box itself is drawn as black.
The output figure above illustrates some key differences between this new definition from the conventional one:
- SDF-L1 is not defined inside the box
- There is a left-center-right separation along the width dimension
- Within the central band of the width dimension, another top-center-bottom separation
One possible use case of such a design choice will be shown in a later post. I’m sure it could be proven useful in many other situations. When it comes to math, there is always going to be some use cases even for the most seemingly useless things.
5. Summary
This post goes through the derivation of signed distance function (SDF) with respect to oriented boxes in 2D.
I also showed Python implementations with some examples.
Lastly, a modified SDF-to-oriented-2D-box definition is presented, where the distance metric is changed from L2-norm to L1-norm (but with signs). One application of the such a new definition will be given in a follow-up post.
Created: 2022-09-24 Sat 23:19