Understanding transposed convolutions in PyTorch
Table of Contents
1 The problem
PyTorch’s documentation on the transposed convolution modules
(nn.ConvTransposexd, x being 1, 2 or 3) is bloody confusing!
This is to a large part due to their implicit switching of context when using terms like “input” and “output”, and overloads of terms like “stride”.
The animated gifs they pointed to, although well-produced, still need some explanation in words.
Let’s work through a derivation and clarify what’s really happening.
2 Derivation and explanation
2.1 The output length equation
The formula given in the doc of nn.ConvTransposexd modules is:
\[ H_{out} = (H_{in}−1)×stride[0]−2×padding[0]+dilation[0]×({kernel_size}[0]−1)+{output_padding}[0]+1 \]
First, let’s introduce some simpler symbols and re-arrange the formula a bit:
\[ o = s(l-1) + d(f-1) + 1 – 2p + p_o \]
where:
- \(o\): output length (in any dimension)
- \(s\): stride, default to 1
- \(l\): input length (in any dimension)
- \(d\): dilation, default to 1
- \(f\): filter/kernel size
- \(p\): padding, default to 0
- \(p_o\): padding onto the output, default to 0
The definitions given above are rather terse, because some of them require more detailed explanations. Let’s start by re-arranging Eq 1 again:
\[ o = [l + (s-1)(l-1)] + [f+(d-1)(f-1)-1] – [2p] + [p_o] \]
This looks more complicated than before, but it will make more sense when we explain how it works.
NOTE that I’m using square brackets \([\,]\) to create 4 groups of terms:
- group-1: \([l + (s-1)(l-1)]\), this is “a measure” of/about the input length. By input I mean input to the transposed conv layer.
- group-2: \([f+(d-1)(f-1)-1]\), this is “a measure” of/about the filter length.
- group-3: \([-2p]\), this is the most confusing term, mostly due to its negative sign. The way to understand it is to treat it as the extra length padded onto the input to the normal conv layer, NOT the input to the transposed conv layer. More on this later.
- group-4: \([p_o]\), this is the extra length padded onto the output from the transposed conv layer. This could be regarded as extra addition to group-1, but it only takes effect when \(s>1\). More on this later.
2.2 Simple case of stride=1, dilation=1, paddings=0
Let’s deal with a simple scenario first.
When \(s=1,\;d=1\;p=0\;p_o=0\), the size equation becomes:
\[ o = [l] + [f-1] \]
In this case, group-1 is \(l\), and group-2 \(f-1\).
One way to understand it is: imagine the filter is sliding across the input sequence. Figure 1 below shows a concrete example where \(l=5\;f=3\).
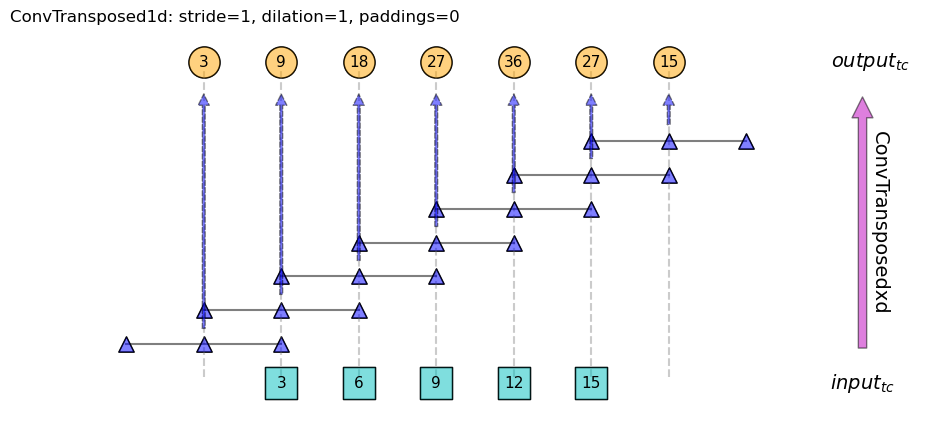

Figure 1: Schematic for 1d transposed convolution. Input sequence is shown as squares at the bottom, output as circles at the top. Filter is [1, 1, 1], represented as triangles.
The filter (triangles) starts from leftmost end, with its last element overlapping
with the 1st element of input (3) . And it ends with a position
where its 1st element overlaps with the last element of input (15).
So, if we focus on the end point of the filter, it steps through the \(l\) positions of the input, when it has overlaps with points in the input (this is group-1), plus an extra \(f-1\) points outside of the input when it has no overlap with the input (this is group-2).
This same counting method will be used throughout:
- group-1 counts the number of steps when the end point of the filter overlaps with the input.
- group-2 counts the extra steps where there is no overlap between the two.
2.3 When stride > 1
To proceed further to include the remaining \(s\), \(d\), \(p\) and \(p_o\) terms, it may be necessary to get some terms and notations straight:
- \(input_{c}\): the input into a normal conv layer, we also use it to denote the length of the input sequence. Similarly for the next 3 terms.
- \(output_{c}\): the output from a normal conv layer.
- \(input_{tc}\): the input into a transposed conv layer.
- \(output_{tc}\): the output from a transposed conv layer.
- \(s_c\): the stride in a normal conv layer, i.e. \(s_c=2\)
means the filter moves 2 cells every time. This is the
strideargument you give to thenn.Convxd()module. - \(s_{tc}\): This is the
strideargument you give to thenn.ConvTransposexd()module. BUT: it shouldn’t be understood as the filter step size in the transposed convolution, instead, treat it as the same as the filter step in the normal conv layer.
Below is a concrete example given in Code block 1. Figure 2 is the screenshot of outputs, and Figure 3 the schematic.
conv = nn.Conv1d(1, 1, kernel_size=3, stride=2, padding=0, dilation=1, bias=False) with torch.no_grad(): conv.weight.data.fill_(1) x = torch.tensor(np.arange(7)).float() x = x.unsqueeze(0) x = x.unsqueeze(0) y = conv(x) print('\n### Normal conv:\n\t', conv) print('Input sequence x:\n\t', x) print('Filter weights:\n\t', conv.weight.data) print('Output sequence y:\n\t', y) transconv = nn.ConvTranspose1d(1, 1, kernel_size=3, stride=2, padding=0, bias=False) with torch.no_grad(): transconv.weight.data.fill_(1) x2 = transconv(y) print('\n### Tranposed conv:\n\t', transconv) print('Input sequence y:\n\t', y) print('Filter weights:\n\t', transconv.weight.data) print('Output sequence x2:\n\t', x2)
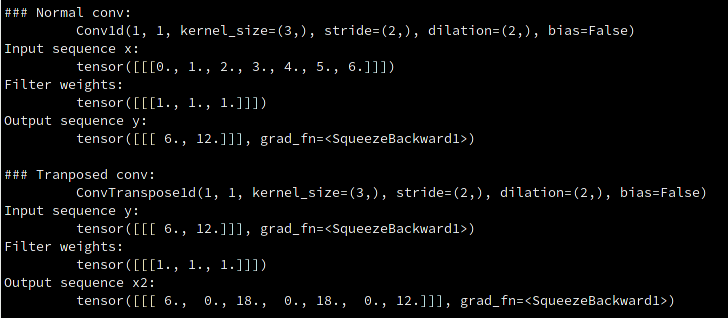


Figure 2: Screenshot of Python code output from Code block 1
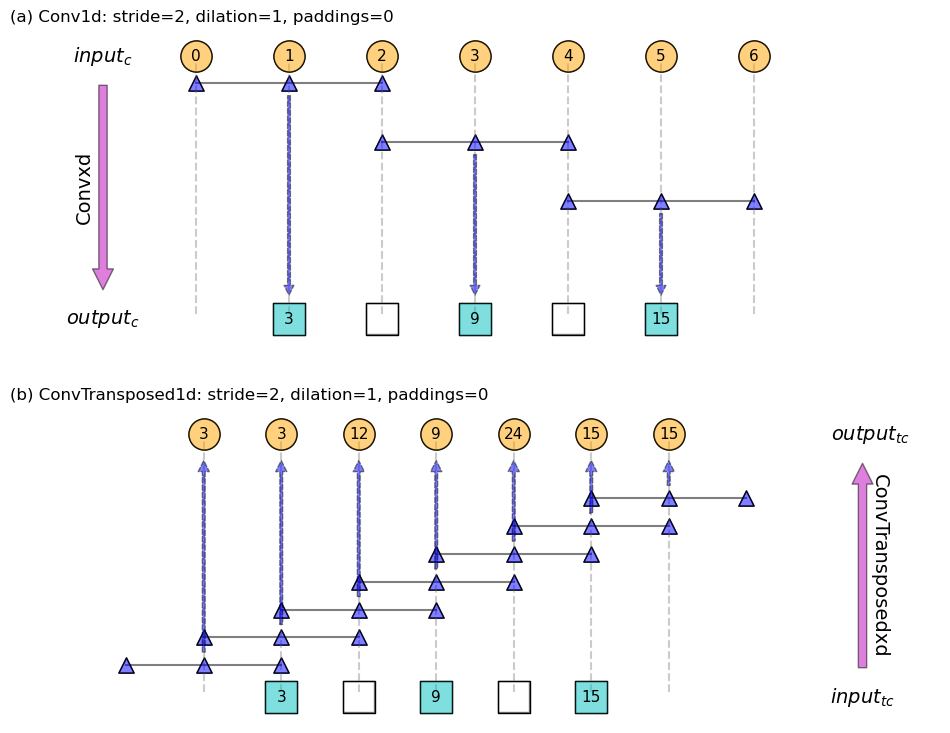

Figure 3: Schematic for (a) 1d normal convolution and (b) transposed convolution, corresponding to the example given in Code block 1. Filter is [1, 1, 1], represented as triangles. Hallow squares denote empty placeholders.
The top row with solid dots is the inputs to a normal conv layer, therefore \(input_{c} = 7\).
From top to bottom, the inputs are convoled with a filter of \(f=3\;s_{c}=2\). This gives the bottom row where solid squares are the outputs from the normal conv layer, therefore \(output_{c}=3\).
Note that I’m adding some hallow squares in the 2nd row to denote the empty slots created by the \(s_{c}=2\) stride.
The way nn.ConvTransposexd is designed in PyTorch is that they
try to make Convxd and ConvTransposexd inverses to each
other (in terms of shape transformations). I found it very
helpful to keep this in mind when understanding transposed convolutions in
PyTorch.
So, the “inverse” operation ConvTransposexd
should map from the bottom row to the top, with a consistent set of
arguments.
That’s to say, the argument \(s_{tc}\) we give to
nn.ConvTransposexd(), is actually the same as \(s_{c}\) that we used
in its “inverse” function nn.Convxd(), and it DOES NOT describe the
filter movement step in the transposed convolution!
Let’s see whether this matches the equation. With \(s_{tc}=2\), we “dilute”/”interleave” (I’m deliberately avoiding overloading the term “dilate”) the \(input_{tc}\) with \(s_{tc}-1=1\) empty slots (shown as hallow squares). So there will be \((s_{tc}-1) * (l-1)\) such empty placeholders added.
And, the filter in the transposed convolution still moves 1 step at a time, regardless the \(s_{tc}\) value. This gives the value for group-1: \(l + (s_{tc}-1) * (l-1)\)
Also because the filter moves 1 step a time, the term from group-2 is still \(f – 1\).
So, for \(s_{tc}>1\), \(d=1\), \(p=0\), \(p_o=0\), the output size is
\[ o = [l + (s_{tc}-1) * (l-1)] + [f-1] \]
In the example shown in Figure 3, \(output_{tc}=7\), and we indeed achieve “an inverse” operation.
The 2 key points here:
- “stride” should be understood as describing the number of interleaving empty slots inserted into the input into the transposed conv layer, or the filter movement step in the normal conv layer.
- Even when “stride” > 1, the filter still moves 1 step at a time.
Both of these are already illustrated in these animated gifs.
2.4 When stride > 1, dilate > 1
This is a relatively easy part: the explanation given by PyTorch’s doc is actually rather to the point: “Spacing between kernel elements”.
This means that for a filter with length \(f\), we add \(d-1\) number of empty slots for each of the \(f-1\) intervals within the filter, giving the new group-2 number: \(f + (d-1)(f-1) -1\). And group-1 is not affected.
Below is the snippet that generates a concrete example using code block 2, and Figure 4 shows the output. Figure 5 gives a schematic.
conv = nn.Conv1d(1, 1, kernel_size=3, stride=2, padding=0, dilation=2, bias=False) with torch.no_grad(): conv.weight.data.fill_(1) x = torch.tensor(np.arange(7)).float() x = x.unsqueeze(0) x = x.unsqueeze(0) y = conv(x) print('\n### Normal conv:\n\t', conv) print('Input sequence x:\n\t', x) print('Filter weights:\n\t', conv.weight.data) print('Output sequence y:\n\t', y) transconv = nn.ConvTranspose1d(1, 1, kernel_size=3, stride=2, padding=0, dilation=2, bias=False) with torch.no_grad(): transconv.weight.data.fill_(1) x2 = transconv(y) print('\n### Tranposed conv:\n\t', transconv) print('Input sequence y:\n\t', y) print('Filter weights:\n\t', transconv.weight.data) print('Output sequence x2:\n\t', x2)



Figure 4: Screenshot of Python code output from Code block 2
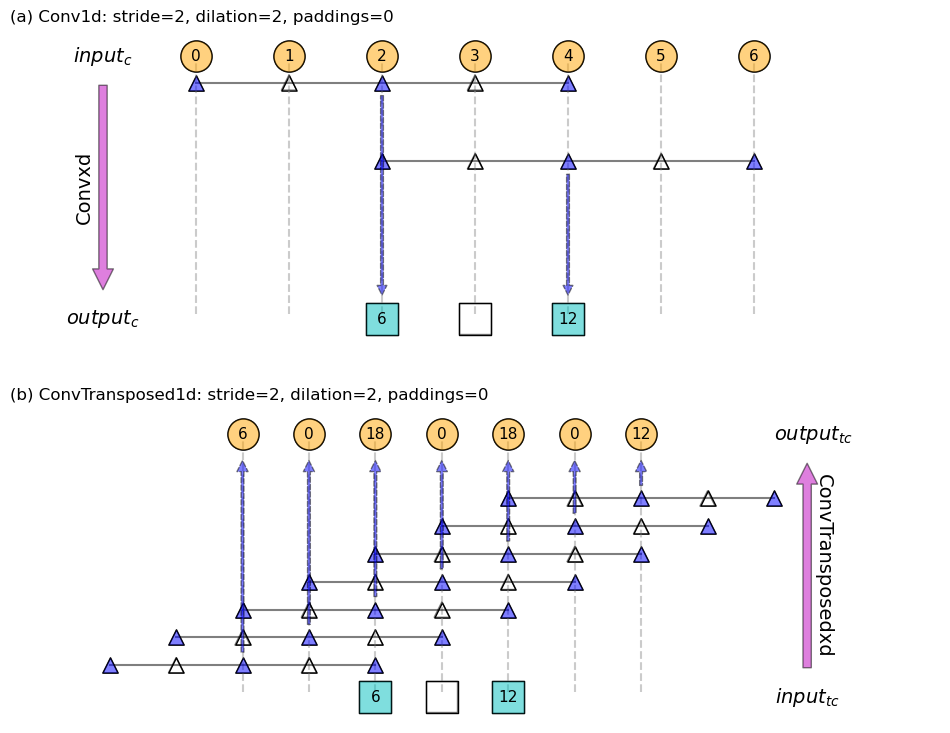

Figure 5: Schematic for (a) 1d normal convolution and (b) transposed convolution, corresponding to the example given in Code block 2. Filter is [1, 1, 1], represented as solid triangles, and dilated places in the filter are represented as hallow triangles. Hallow squares denote empty placeholders.
- from top to bottom is the normal convolution.
- from bottom to top is the transposed convolution.
- \(input_{c} = 7\).
- for the normal convolution: \(f = 3\), \(d = 2\), \(s_{c}=2\).
- this gives \(output_{c}=2\).
- for the transposed convolution: \(f = 3\), \(d = 2\), \(s_{tc}=2\). Remember: the filter still moves 1 step at a time!
- this gives \(output_{tc} = 7\). Again, we achieved “an inverse” operation.
2.5 When stride > 1, dilate > 1, padding > 1
I think this the worst part of all. To quote PyTorch’s doc:
“
padding(intortuple, optional) –dilation * (kernel_size - 1) - paddingzero-padding will be added to both sides of each dimension in the input. Default: 0″
Not sure how you feel about it, this makes NO sense to me.
The extra note helps (only by a little):
“The
paddingargument effectively addsdilation * (kernel_size - 1) - paddingamount of zero padding to both sizes of the input. This is set so that when aConv2dand aConvTranspose2dare initialized with same parameters, they are inverses of each other in regard to the input and output shapes.”
The dilation * (kernel_size - 1) - padding part is awfully
confusing, I think it would be better off if they just deleted that.
This sentence does shed some light: “This is set so that when a
Conv2d and a ConvTranspose2d are initialized with same parameters,
they are inverses of each other in regard to the input and output
shapes.”
So it’s helpful to look at the paired operations. The Code block 2 below gives an example, and Figure 6 the output, Figure 7 an schematic.
conv = nn.Conv1d(1, 1, kernel_size=3, stride=2, padding=1, dilation=2, bias=False) with torch.no_grad(): conv.weight.data.fill_(1) x = torch.tensor(np.arange(7)).float() x = x.unsqueeze(0) x = x.unsqueeze(0) y = conv(x) print('\n### Normal conv:\n\t', conv) print('Input sequence x:\n\t', x) print('Filter weights:\n\t', conv.weight.data) print('Output sequence y:\n\t', y) transconv = nn.ConvTranspose1d(1, 1, kernel_size=3, stride=2, padding=1, dilation=2, bias=False) with torch.no_grad(): transconv.weight.data.fill_(1) x2 = transconv(y) print('\n### Tranposed conv:\n\t', transconv) print('Input sequence y:\n\t', y) print('Filter weights:\n\t', transconv.weight.data) print('Output sequence x2:\n\t', x2)
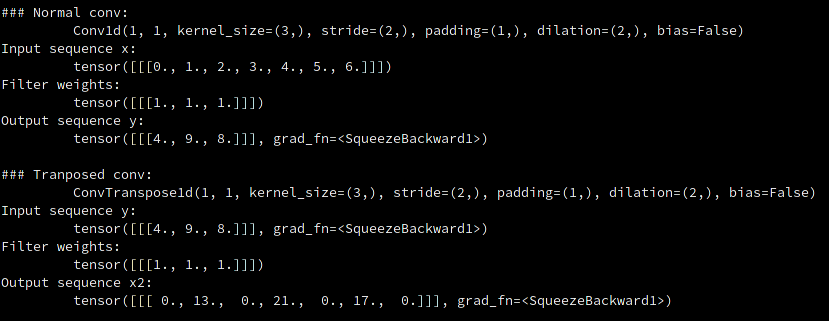

Figure 6: Screenshot of Python code output from Code block 2
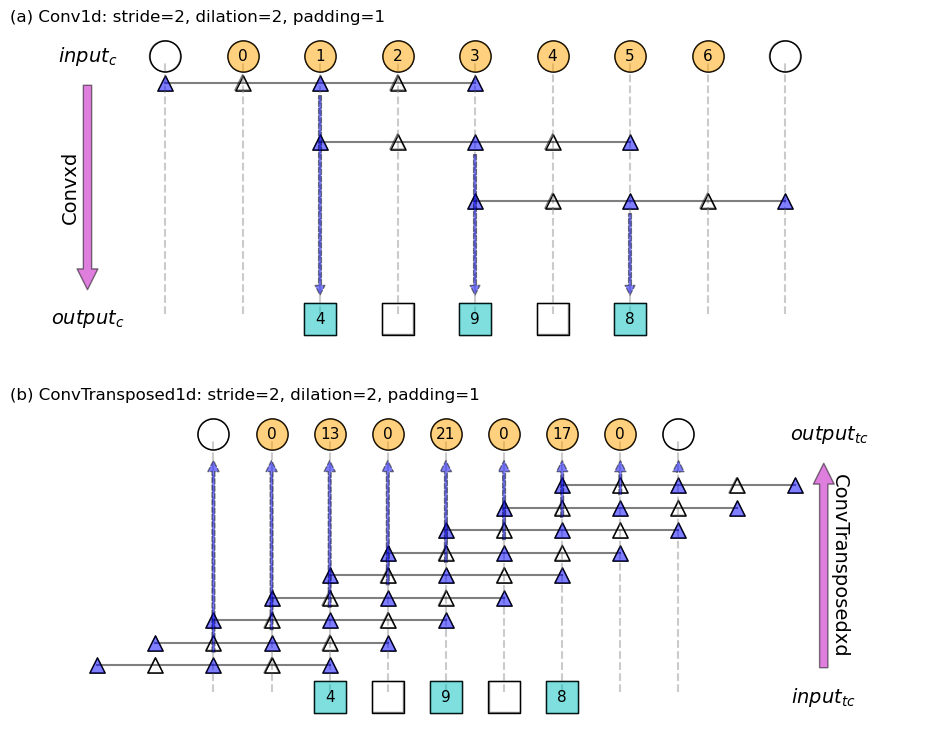

Figure 7: Schematic for (a) 1d normal convolution and (b) transposed convolution, corresponding to the example given in Code block 2. Filter is [1, 1, 1], represented as solid triangles, dilated places in the filter are represented as hallow triangles. Hallow squares denote empty placeholders. Hallow circles denote padded inputs during the normal convolution, or removed outputs during the transposed convolution.
- from top to bottom is the normal convolution
- from bottom to top is the transposed convolution
- \(input_{c} = 7\)
- for the normal convolution: \(f = 3\), \(d = 2\), \(s_{c}=2, p=1\)
- this gives \(output_{c}=3\)
- for the transposed convolution: \(f = 3\), \(d = 2\), \(s_{tc}=2\), \(p=1\). Remember: the filter still moves 1 step at a time!
This gives the \(output_{tc} = [l + (s-1)(l-1)] + [f + (d-1)(f-1) -1] + [-2p] = [5] + [4] – [2] = 7\).
Again, we achieved “an inverse” operation.
Therefore, by “padding”, they actually meant the padding added onto
the “forward”/”normal” convolution of nn.Convxd(), and you need to copy that same
number into nn.ConvTransposexd(), such that these 2 operations are
“inverses” to each other.
Let’s walk through the computations in more details:
we still start the transposed convolution from the 1st dot product:
\[ [1, 0, 1, 0, 1] \cdot [nan, nan, nan, nan, 4]^{T} = 4 \]
where \(nan\) denotes out-of-bound placeholders in the \(input_{tc}\).
But, that output is NOT included, contributing a \(-p\) to the total count. And we move to the next window position (Remember: the filter still moves 1 step at a time! )
\[ [1, 0, 1, 0, 1] \cdot [nan, nan 0, 4, 0]^{T} = 0 \]
Then the next step:
\[ [1, 0, 1, 0, 1] \cdot [nan, 0, 4, 0, 9]^{T} = 13 \]
And next:
\[ [1, 0, 1, 0, 1] \cdot [0, 4, 0, 9, 0]^{T} = 0 \]
On the right most end, we should have
\[ [1, 0, 1, 0, 1] \cdot [8, nan, nan, nan, nan]^{T} = 8 \]
But this output \(8\) is also not included, and is the remaining part of the \([-2p]\) term.
2.6 When stride > 1, dilate > 1, padding > 1, output padding > 1
The extra \(p_o\) term, as our group-4 is added to the previous 3 groups, completing our Eq 1:
\[ o = [l + (s-1)(l-1)] + [f+(d-1)(f-1)-1] – [2p] + [p_o] \]
PyTorch’s doc describes it as the “additional size added to one side of each dimension in the output shape”.
NOTE that is NOT padding 0s to the “diluted”/”interleaved” \(input_{tc}\), otherwise the layer output will always has a rim of 0s around the edges.
This is again for the purpose of making normal and transposed convolutions “inverse” operations. During the normal convolution, the output size is computed as:
\[ output_{c} = [\frac{input_{c} + 2p – f}{s}] + 1 \]
where \([]\) is the floor function. So, it is possible that different \(input_{c}\) values get mapped onto a same \(output_c\), e.g.
\[ [\frac{7 + 2 \times 1 – 3}{2}] + 1 = [\frac{8 + 2 \times 1 – 3}{2}] + 1 = 4 \]
In such cases, output_padding allows one to add the extra few
elements such that \(input_{c} = output_{tc}\). Therefore,
output_padding only works when \(s_{tc} > 1\).
Using our last example (Code block 2) but with the extra output_padding=1 parameter
added, you could see that the trailing value \(8\) that was previously
removed as a part of the \(-2p\) term, is now reserved, giving \(output_{tc}=8\).
conv = nn.Conv1d(1, 1, kernel_size=3, stride=2, padding=1, dilation=2, bias=False) with torch.no_grad(): conv.weight.data.fill_(1) x = torch.tensor(np.arange(7)).float() x = x.unsqueeze(0) x = x.unsqueeze(0) y = conv(x) print('\n### Normal conv:\n\t', conv) print('Input sequence x:\n\t', x) print('Filter weights:\n\t', conv.weight.data) print('Output sequence y:\n\t', y) transconv = nn.ConvTranspose1d(1, 1, kernel_size=3, stride=2, padding=1, dilation=2, output_padding=1,bias=False) with torch.no_grad(): transconv.weight.data.fill_(1) x2 = transconv(y) print('\n### Tranposed conv:\n\t', transconv) print('Input sequence y:\n\t', y) print('Filter weights:\n\t', transconv.weight.data) print('Output sequence x2:\n\t', x2)
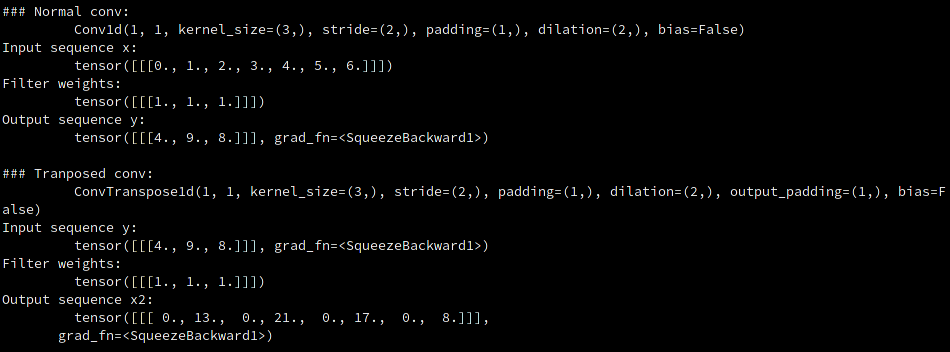

Figure 8: Screenshot of Python code output from Code block 2
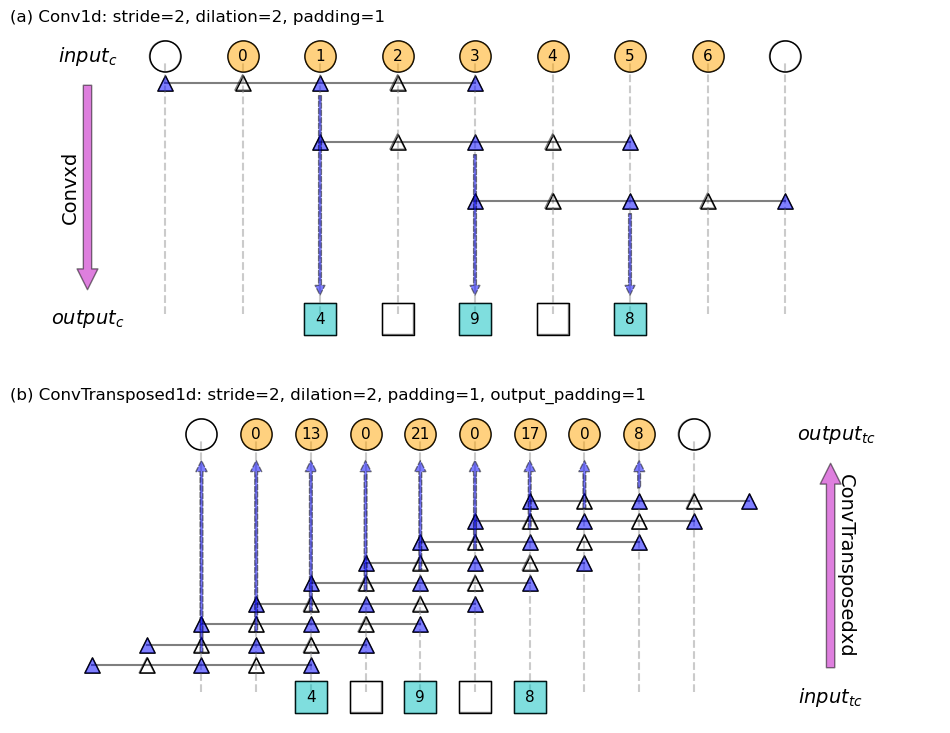

Figure 9: Schematic for (a) 1d normal convolution and (b) transposed convolution, corresponding to the example given in Code block 2. Filter is [1, 1, 1], represented as solid triangles, dilated places in the filter are represented as hallow triangles. Hallow squares denote empty placeholders. Hallow circles denote padded inputs during the normal convolution, or removed outputs during the transposed convolution.
3 Summary
We walked through derivations of the computations in transposed convolutions in PyTorch, and clarified some confusions in their documentation, much of which stem from implicit changes of context and overloads of terms.
It is helpful to keep in mind PyTorch’s design choice that normal conv layers and transposed conv layers are “inverse” operations to each other, in that they revert the shape of a tensor.
In fact, for some input arguments to a nn.ConvTransposexd module,
it is easier to mentally read them as the input arguments to
nn.Convxd, and think about them as:
“what arguments would a forward convolution use to get the current tensor at hand, that I am now feeding into a transposed convolution”.
These arguments include:
- stride
- padding
Despite the same names, these arguments mean rather different things
in nn.Convxd and nn.ConvTransposexd, creating great confusion to
the output size formula. The overloading of argument names helps
maintain consistency in the code API (maybe?), but the explanations
could certainly be made better.
With the above confusions cleared, we give a break-down of the formula given in PyTorch’s documentation:
\[ o = s(l-1) + d(f-1) + 1 – 2p + p_o = [l + (s-1)(l-1)] + [f+(d-1)(f-1)-1] – [2p] + [p_o] \]
where:
- \(o\): output length (in any dimension).
- \(s\): the stride used in the normal or forward convolution. The input to a transposed conv layer is “diluted”/”interleaved” with \(s-1\) number of 0s. Default to 1.
- \(l\): length of input to the transposed conv layer.
- \(d\): dilation of the filter, i.e. the filter is interleaved with \(d-1\) number of 0s. Default to 1.
- \(f\): filter size (before dilation).
- \(p\): padding used in the normal convolution. \(2p\) number of elements from both ends of the output from a transposed conv layer are removed, effectively “undo” the padding performed in the normal convolution. Default to 0
- \(p_o\): extra length added to the output from the transposed conv layer. Only used when \(s>1\). This is to clarify the size ambiguity created by the floor function in computing the output size in a normal convolution.
The basic idea of the derivation is to count the output elements as 2 parts:
- counts the number of steps when the end point of the filter overlaps with the input. This corresponds to our group-1 term: \([l + (s-1)(l-1)]\).
- counts the extra steps where there is no overlap between the filter and the input. This is our group-2 term: \([f+(d-1)(f-1)-1]\).
The extra group-3 of \(-2p\), and group-4 of \(p_o\), are due to a design choice of PyTorch to make the normal and transposed convolutions inverse operations to each other.
Created: 2022-05-04 Wed 20:09


[…] one can also work out the dilation and output_padding arguments relatively easily. I’ve written a blog on this, in case anyone is […]