• \(f^{(l)}\): height and width of the convolution kernel/filter.
• \(n^{(l)}_c\): number of filters in the convolution layer.
• \(n^{(l-1)}_H \times n^{(l-1)}_W \times n^{(l-1)}_c\): size of the input to the convolution layer, i.e. activation of layer \(l-1\), as the product of height (\(n^{(l-1)}_H\)), width (\(n^{(l-1)}_W\)) and number of channels (\(n^{(l-1)}_c\)).
• \(n^{(l)}_H \times n^{(l)}_W \times n^{(l)}_c\): size of the output of the convolution layer.
• \(w^{(l,k)}\): the kth convolution kernel/filter of layer \(l\): \(w^{(l,k)} \in \mathbb{R}^{f^{(l)} \times f^{(l)}}\).
• \(z^{(l,k)}\): convolution result from the kth filter: \(z^{(l,k)} \in \mathbb{R}^{n^{(l)}_H \times n^{(l)}_W}\).
• \(z^{(l)}\): stacked convolution results from all filters: \(z^{(l)} \in \mathbb{R}^{n^{(l)}_H \times n^{(l)}_W \times n^{(l)}_c}\).
• \(b^{(l, k)}\): bias term for the kth filter in the layer: \(b^{(l,k)} \in \mathbb{R}\).
• \(b^{(l)}\): bias term for all the filters in the layer: \(b^{(l)} \in \mathbb{R}^{n^{(l)}_c}\).
• \(a^{(l,k)}\): result of the activation function for the kth filter in the layer: \(a^{(l, k)} \in \mathbb{R}^{n^{(l)}_H \times n^{(l)}_W}\).
• \(a^{(l)}\): result of the activation function for all the filters in the layer: \(a^{(l)} \in \mathbb{R}^{n^{(l)}_H \times n^{(l)}_W \times n^{(l)}_c}\).

Take for instance the convolution layer shown in Figure 1 below. The input to the layer is denoted \(a^{(l-1)}\), which is also the activation of layer \(l-1\). In the case shown in Figure xxx \(a^{(l-1)}\) is a 2D array, but recall that in general \(a^{(l-1)}\) is a 3D data volume.

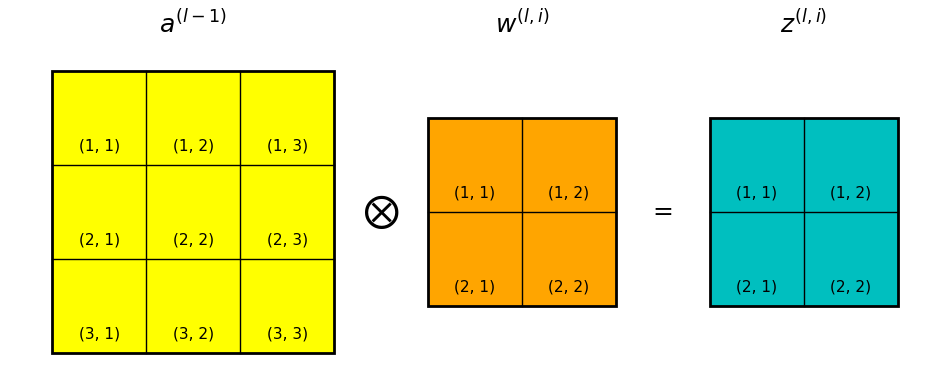
\(w^{(l,k)}\) is the kth convolution kernel/filter in the convolution layer.

The convolution process is given as:

\[
z^{(l,k)} = a^{(l-1)} \otimes w^{(l,k)}
\]

where \(\otimes\) is the convolution operator.

Then a bias term \(b^{(l,k)} \in \mathbb{R}\) is added to the convolution result:

\[
z^{(l,k)} = a^{(l-1)} \otimes w^{(l,k)} + b^{(l,k)}
\]

Then, the convolution result is passed to an activation function \(g()\):

\[
a^{(l,k)} = g(z^{(l,k)}) = g(a^{(l-1)} \otimes w^{(l,k)} + b^{(l,k)})
\]

After repeating the same process for all of the \(n^{(l)}_c\) filters in the layer and stacking up the results, the output of the convolution layer is \(a^{(l)} \in \mathbb{R}^{n^{(l)}_H \times n^{(l)}_W \times n^{(l)}_c}\).

Finally, we denote the loss function of the CNN as \(J\), and the error term of layer \(l\) as:

\[
\frac{\partial J}{\partial z^{(l)}} \equiv \delta^{(l)}
\]

Let’s write out the convolution process of \(z^{(l)} = a^{(l-1)} \otimes w^{(l)}\):

\[
\left\{\begin{matrix}
z_{1,1} = & a_{1,1} w_{1,1} + a_{1,2} w_{1,2} + a_{2,1} w_{2,1} + a_{2,2} w_{2,2} \\
z_{1,2} = & a_{1,2} w_{1,1} + a_{1,3} w_{1,2} + a_{2,2} w_{2,1} + a_{2,3} w_{2,2} \\
z_{2,1} = & a_{2,1} w_{1,1} + a_{2,2} w_{1,2} + a_{3,1} w_{2,1} + a_{3,2} w_{2,2} \\
z_{2,2} = & a_{2,2} w_{1,1} + a_{2,3} w_{1,2} + a_{3,2} w_{2,1} + a_{3,3} w_{2,2} \\
\end{matrix}\right.
\] [Eq. 1]

To update the weights we need to compute their gradients \(\frac{\partial J}{\partial w^{(l)}_{i,j}}\), where \(l\) denotes layer \(l\), \(i\) and \(j\) denote the row/column indices of a number in the filter.

By applying the chain rule on the 1st element of the weight matrix \(w_{1,1}\) and using Equation 1:

\[
\frac{\partial J}{\partial w_{1,1}} = \frac{\partial J}{\partial z_{1,1}} \frac{\partial z_{1,1}}{\partial w_{1,1}} +
\frac{\partial J}{\partial z_{1,2}} \frac{\partial z_{1,2}}{\partial w_{1,1}} +
\frac{\partial J}{\partial z_{2,1}} \frac{\partial z_{2,1}}{\partial w_{1,1}} +
\frac{\partial J}{\partial z_{2,2}} \frac{\partial z_{2,2}}{\partial
w_{1,1}}
\] [Eq 2]

Note I’m omitting the superscript \(^{(l)}\) for all the \(w\) and \(z\) terms in the above equation.

Notice that \(\frac{\partial J}{\partial z_{1,1}}\) is \(\delta_{1,1}\) by definition, and \(\frac{\partial z_{1,1}}{\partial w_{1,1}} = a_{1,1}\) from Equation 1. We can similarly replace all other terms in Equation 2 to get:

\[
\frac{\partial J}{\partial w_{1,1}} = \delta_{1,1} a_{1,1} +
\delta_{1,2} a_{1,2} +
\delta_{2,1} a_{2,1} +
\delta_{2,2} a_{2,2}
\]

That gives the gradient for the first element in the weight matrix. Repeating the same process we get the gradients for all the elements in weight \(w^{(l)}\):

\[
\left\{\begin{matrix}
\frac{\partial J}{\partial w^{(l)}_{1,1}} = & \delta^{(l)}_{1,1} a^{(l-1)}_{1,1} + \delta^{(l)}_{1,2} a^{(l-1)}_{1,2} + \delta^{(l)}_{2,1} a^{(l-1)}_{2,1} + \delta^{(l)}_{2,2} a^{(l-1)}_{2,2} \\
\frac{\partial J}{\partial w^{(l)}_{1,2}} = & \delta^{(l)}_{1,1} a^{(l-1)}_{1,2} + \delta^{(l)}_{1,2} a^{(l-1)}_{1,3} + \delta^{(l)}_{2,1} a^{(l-1)}_{2,2} + \delta^{(l)}_{2,2} a^{(l-1)}_{2,3} \\
\frac{\partial J}{\partial w^{(l)}_{2,1}} = & \delta^{(l)}_{1,1} a^{(l-1)}_{2,1} + \delta^{(l)}_{1,2} a^{(l-1)}_{2,2} + \delta^{(l)}_{2,1} a^{(l-1)}_{3,1} + \delta^{(l)}_{2,2} a^{(l-1)}_{3,2} \\
\frac{\partial J}{\partial w^{(l)}_{2,2}} = & \delta^{(l)}_{1,1} a^{(l-1)}_{2,2} + \delta^{(l)}_{1,2} a^{(l-1)}_{2,3} + \delta^{(l)}_{2,1} a^{(l-1)}_{3,2} + \delta^{(l)}_{2,2} a^{(l-1)}_{3,3} \\
\end{matrix}\right.
\]

I’ve added all superscripts to make it clearer which term is from which layer.

It is a pretty complicated equation set at first look. However, it turns out that it can be expressed more neatly as:

\[
\frac{\partial J}{\partial w^{(l)}} = a^{(l-1)} \otimes \delta^{(l)}
\]

[Eq 3]

namely, a convolution between the error term of the layer \(\delta^{(l)}\) and the input to the layer \(a^{(l-1)}\).

Compare this with the gradient computation in an ordinary neural network layer, where

\[
\frac{\partial J}{\partial \theta^{(l)}} = \delta^{(l)} \cdot a^{(l-1)^T}
\]

we have a similar structure: gradients of a weight (\(\frac{\partial J}{\partial \theta^{(l)}}\)) in a layer is proportional to its input (\(a^{(l-1)}\)) and the error of the output (\(\delta^{(l)}\)).

From Equation 3, we see that to compute the gradients for the weights in a layer, we need to know the inputs into the layer (\(a^{(l-1)}\)), which we can get by saving a copy during the forward propagation process; and the error term \(\delta^{(l)}\) of the layer. For the latter we need to propagate the error all the way from the last layer in the network backwards. This is derived in the next part.

We now derive the process of propagating the error backwards across a convolution layer. Using again the schematic in Figure 1, we are looking for an expression of \(\delta^{(l-1)}\), given an in-coming error of \(\delta^{(l)}\).

Recall that the error term is defined as \(\delta^{(l-1)} \equiv \frac{\partial J}{\partial z^{(l-1)}}\).

Using the chain rule, we get:

\[
\delta^{(l-1)} \equiv \frac{\partial J}{\partial z^{(l-1)}} = \frac{\partial J}{\partial a^{(l-1)}} \frac{\partial a^{(l-1)}}{\partial z^{(l-1)}}
\]

[Eq 4]

Note that \(\frac{\partial a^{(l-1)}}{\partial z^{(l-1)}}\) is the derivative of the activation function on \(z^{(l-1)}\):

\[
\frac{\partial a^{(l-1)}}{\partial z^{(l-1)}} = g'(z^{(l-1)})
\]

therefore, it is useful to also save a copy of \(z^{(l-1)}\) during the forward propagation process, and it is also required to know the derivative of the activation function.

Then we need to work out the \(\frac{\partial J}{\partial a^{(l-1)}}\) term in Equation 4.

Notice that \(a^{(l-1)}\) is the input to the convolution layer. Using the chain rule again on the 1st element of \(a^{(l-1)}\):

\[
\frac{\partial J}{\partial a^{(l-1)}_{1,1}} = \frac{\partial J}{\partial z^{(l)}_{1,1}} \frac{\partial z^{(l)}_{1,1}}{\partial a^{(l-1)}_{1,1}} = \delta^{(l)}_{1,1} w^{(l)}_{1,1}
\]

where \(\frac{\partial J}{\partial z^{(l)}_{1,1}} = \delta^{(l)}_{1,1}\) is from the definition of \(\delta\), and \(\frac{\partial z^{(l)}_{1,1}}{\partial a^{(l-1)}_{1,1}} = w^{(l)}_{1,1}\) is from Equation 1.

Write out all elements in \(\frac{\partial J}{\partial a^{(l-1)}}\), we have:

\[
\left\{\begin{matrix}
\frac{\partial J}{\partial a^{(l-1)}_{1,1}} = & \delta^{(l)}_{1,1} w^{(l)}_{1,1} \\
\frac{\partial J}{\partial a^{(l-1)}_{1,2}} = & \delta^{(l)}_{1,1} w^{(l)}_{1,2} + \delta^{(l)}_{1,2}w^{(l)}_{1,1} \\
\frac{\partial J}{\partial a^{(l-1)}_{1,3}} = & \delta^{(l)}_{1,2} w^{(l)}_{1,2} \\
\frac{\partial J}{\partial a^{(l-1)}_{2,1}} = & \delta^{(l)}_{1,1} w^{(l)}_{2,1} + \delta^{(l)}_{2,1}w^{(l)}_{1,1} \\
\cdots & \cdots \\
\frac{\partial J}{\partial a^{(l-1)}_{3,3}} = & \delta^{(l)}_{2,2} w^{(l)}_{2,2} \\
\end{matrix}\right.
\]

[Eq 5]

It is another monstrous equation set. Fortunately, it can be expressed more neatly again as a convolution:

\[
\frac{\partial J}{\partial a^{(l-1)}} = \delta^{(l)} \otimes_f Rot_{180}(w^{(l)})
\]

where:

• \(\otimes_f\) denotes a “full mode” convolution. See the Convolution modes section in this post for an illustration. In a nutshell, in a “full mode” convolution we compute a dot product between the convolution kernel and the underlying data subset whenever they have any overlap, and as a result, the result from a “full mode” convolution has a larger size than the input. This is also the case as shown in Figure 1.
• \(Rot_{180}()\) is a function that rotates a matrix by 180 degree, or equivalently, flips the matrix horizontally and vertically. Note that in the case of 3D convolution, this does not flip the channel dimension.

Given Equation 5 and Equation 4, we get the formula for error back propagation across a convolution layer:

\[
\delta^{(l-1)} = \delta^{(l)} \otimes_f Rot_{180}(w^{(l)}) \odot g'(z^{(l-1)})
\]

[Eq 6]

Again, it is interesting to note a similar structure in the back propagation in an ordinary neural network:

\[
\delta^{(l-1)} = \theta^{(l)^T} \cdot \delta^{(l)} \odot g'(z^{(l-1)})
\]

• the input is a 3D data volume: \(a^{(l-1)} \in \mathbb{R}^{3 \times 3 \times 3}\).
• there are \(4\) filters in the convolution layer, each is a 3D array: \(w^{(l, k)} \in \mathbb{R}^{2 \times 2 \times 3}, \; k=1,2,3,4\).
• for each filter, the convolution produces a 2D slab: \(z^{(l, k)} \in \mathbb{R}^{2 \times 2}, \; k=1,2,3,4\).
• After stacking up all 4 convolution results, the total convolution result is \(z^{(l)} \in \mathbb{R}^{2 \times 2 \times 4}\).

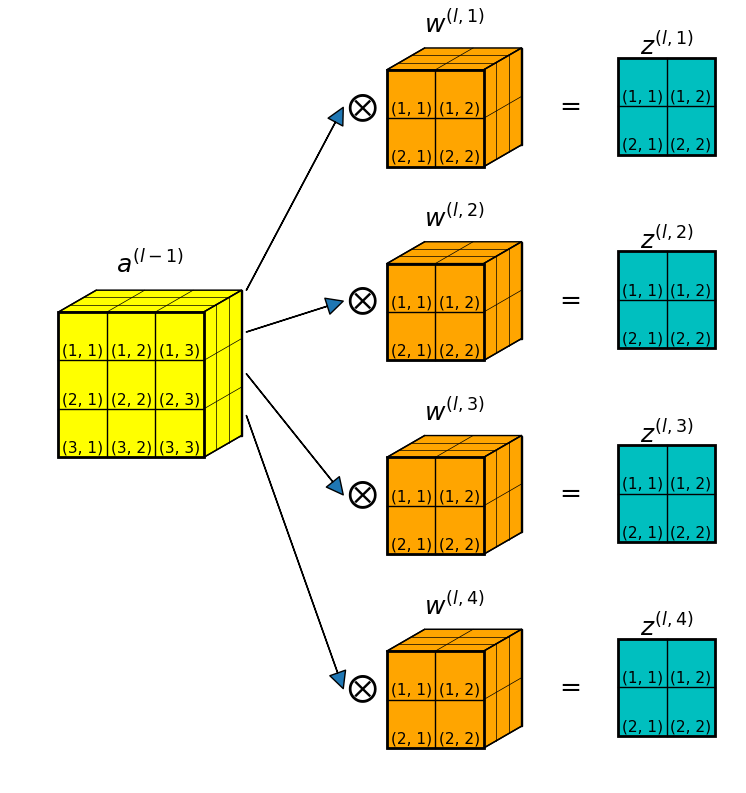
Equation 3 in the above section shows that to get the gradients of filter weights in a 2D convolution with a single filter, we do a convolution between the input (\(a^{(l-1)}\)) and the error (\(\delta^{(l)}\)).

In the case of 3D convolution, it is noticed that there exists a branching-off of the “data flow”: each filter \(w^{(l,k)}\) produces a separate convolution result that is independent to all other filters. Consequently, the weight gradients are computed independently for each filter, using the shared input \(a^{(l-1)}\) and the corresponding error term \(\delta^{(l,k)}\):

\[
\frac{\partial J}{\partial w^{(l, k)}} = a^{(l-1)} \otimes
\delta^{(l,k)}, \; k=1,2,3,4
\]

[Eq 7]

Note that the shape of \(a^{(l-1)}\) is \(3 \times 3 \times 3\), that of \(\delta^{(l,k)}\) is \(2 \times 2 \times 1\). Therefore the convolution is done 3 times, each for a different channel. This way, we recover the correct shape of the filter: \(w^{(l, k)} \in \mathbb{R}^{2 \times 2 \times 3}\).

• the error of the layer output \(\delta^{(l)}\),
• the (rotated) corresponding filter \(Rot_{180}(w^{(l)})\), and
• the derivative of the input activation function \(g'(z^{(l-1)})\).

In the case of 3D convolution with multiple filters, the forward pass is a “diverging” flow pattern (see Figure 2), therefore, the backward propagation is a “converging” flow: errors from all filters contribute to the error term of \(\delta^{(l-1)}\):

\[
\delta^{(l-1)} = \sum_{k=1}^4 [ \delta^{(l,k)} \otimes_f Rot_{180}(w^{(l,k)}) \odot g'(z^{(l-1)})]
\]

[Eq 8]

Again, notice that the shape of \(\delta^{(l,k)}\) is \(2 \times 2 \times 1\), that of \(w^{(l,k)}\) is \(2 \times 2 \times 3\). Therefore, the convolution is performed 3 times, recovering the channel dimension of length \(3\).

For a convolution layer with \(n^{(l)}_c\) filters, the bias term is a vector of length \(n^{(l)}_c\): \(b^{(l)} \in \mathbb{R}^{n^{(l)}_c}\).

Given

\[
z^{(l,k)} = a^{(l-1)} \otimes w^{(l,k)} + b^{(l,k)}
\]

the bias term in filter \(k\) contributes to all the elements in the error term of \(\delta^{(l,k)}\), therefore, the derivative wrt to bias is given as:

\[
\frac{\partial J}{\partial b^{(l,k)}} = \sum_i \sum_j \frac{\partial J}{\partial z^{(l,k)}_{i,j}} \frac{\partial z^{(l,k)}_{i,j}}{\partial b^{(l,k)}} = \sum_i \sum_j \delta^{(l,k)}_{i,j}
\]

[Eq 9]

def fullConv3D(var, kernel, stride):
    '''Full mode 3D convolution using stride view.

    Args:
        var (ndarray): 2d or 3d array to convolve along the first 2 dimensions.
        kernel (ndarray): 2d or 3d kernel to convolve. If <var> is 3d and <kernel>
            is 2d, create a dummy dimension to be the 3rd dimension in kernel.
    Keyword Args:
        stride (int): stride along the 1st 2 dimensions. Default to 1.
    Returns:
        conv (ndarray): convolution result.

    Note that the kernel is not filpped inside this function.
    '''
    stride = int(stride)
    ny, nx = var.shape[:2]
    ky, kx = kernel.shape[:2]
    # interleave 0s
    var2 = interLeave(var, stride-1, stride-1)
    # pad boundaries
    nout, pad_left, pad_right = compSize(ny, ky, stride)
    var2 = padArray(var2, pad_left, pad_right)
    # convolve
    conv = conv3D3(var2, kernel, stride=1, pad=0)

    return conv

def interLeave(arr, sy, sx):
    '''Interleave array with rows/columns of 0s.

    Args:
        arr (ndarray): input 2d or 3d array to interleave in the first 2 dimensions.
        sy (int): number of rows to interleave.
        sx (int): number of columns to interleave.
    Returns:
        result (ndarray): input <arr> array interleaved with 0s.

    E.g.
        arr = [[1, 2, 3],
               [4, 5, 6],
               [7, 8, 9]]
        interLeave(arr, 1, 2) ->

        [[1, 0, 0, 2, 0, 0, 3],
         [0, 0, 0, 0, 0, 0, 0],
         [4, 0, 0, 5, 0, 0, 6],
         [0, 0, 0, 0, 0, 0, 0],
         [7, 0, 0, 8, 0, 0, 9]]
    '''

    ny, nx = arr.shape[:2]
    shape = (ny+sy*(ny-1), nx+sx*(nx-1))+arr.shape[2:]
    result = np.zeros(shape)
    result[0::(sy+1), 0::(sx+1), ...] = arr
    return result

def compSize(n, f, s):
    '''Compute the shape of a full convolution result

    Args:
        n (int): length of input array x.
        f (int): length of kernel.
        s (int): stride.
    Returns:
        nout (int): lenght of output array y.
        pad_left (int): number padded to the left in a full convolution.
        pad_right (int): number padded to the right in a full convolution.

    E.g. x = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
    f = 3, s = 2.
    A full convolution is done on [*, *, 0], [0, 1, 2], [2, 3, 4], ..., [6, 7, 8],
    [9, 10, *]. Where * is missing outside of the input domain.
    Therefore, the full convolution y has length 6. pad_left = 2, pad_right = 1.
    '''

    nout = 1
    pad_left = f-1
    pad_right = 0
    idx = 0   # index of the right end of the kernel
    while True:
        idx_next = idx+s
        win_left = idx_next-f+1
        if win_left <= n-1:
            nout += 1
            idx = idx+s
        else:
            break
    pad_right = idx-n+1

    return nout, pad_left, pad_right

def computeGradients(self, delta, act):
    '''Compute gradients of cost wrt filter weights

    Args:
        delta (ndarray): errors in filter ouputs.
        act (ndarray): activations fed into filter.
    Returns:
        grads (ndarray): gradients of filter weights.
        grads_bias (ndarray): 1d array, gradients of biases.

    The theoretical equation of gradients of filter weights is:

        \partial J / \partial W^{(l)} = a^{(l-1)} \bigotimes \delta^{(l)}

    where:
        J : cost function of network.
        W^{(l)} : weights in filter.
        a^{(l-1)} : activations fed into filter.
        \bigotimes : convolution in valid mode.
        \delta^{(l)} : errors in the outputs from the filter.

    Computation in practice is more complicated than the above equation.
    '''

    nc_out = delta.shape[-1]   # number of channels in outputs
    nc_in = act.shape[-1]      # number of channels in inputs

    grads = np.zeros_like(self.filters)

    for ii in range(nc_out):
        deltaii = np.take(delta, ii, axis=-1)
        gii = grads[ii]
        for jj in range(nc_in):
            actjj = act[:, :, jj]
            gij = conv3D3(actjj, deltaii, stride=1, pad=0)
            gii[:, :, jj] += gij
        grads[ii] = gii

    # gradient clip
    gii = np.clip(gii, -self.clipvalue, self.clipvalue)
    grads_bias = np.sum(delta, axis=(0, 1))  # 1d

    return grads, grads_bias

def backPropError(self, delta_in, z):
    '''Back-propagate errors

    Args:
        delta_in (ndarray): delta from the next layer in the network.
        z (ndarray): weighted sum of the current layer.
    Returns:
        result (ndarray): delta of the current layer.

    The theoretical equation for error back-propagation is:

        \delta^{(l)} = \delta^{(l+1)} \bigotimes_f Rot(W^{(l+1)}) \bigodot f'(z^{(l)})

    where:
        \delta^{(l)} : error of layer l, defined as \partial J / \partial z^{(l)}.
        \bigotimes_f : convolution in full mode.
        Rot() : is rotating the filter by 180 degrees, i.e. a kernel flip.
        W^{(l+1)} : weights of layer l+1.
        \bigodot : Hadamard (elementwise) product.
        f() : activation function of layer l.
        z^{(l)} : weighted sum in layer l.

    Computation in practice is more complicated than the above equation.
    '''

    # number of channels of input to layer l weights
    nc_pre = z.shape[-1]
    # number of channels of output from layer l weights
    nc_next = delta_in.shape[-1]

    result = np.zeros_like(z)
    # loop through channels in layer l
    for ii in range(nc_next):
        # flip the kernel
        kii = self.filters[ii, ::-1, ::-1, ...]
        deltaii = delta_in[:, :, ii]
        # loop through channels of input
        for jj in range(nc_pre):
            slabij = fullConv3D(deltaii, kii[:, :, jj], self.stride)
            result[:, :, jj] += slabij

    result = result*dReLU(z)

    return result

    
def dReLU(x):
    '''Gradient of ReLU'''
    return 1.*(x > 0)

def fullConv3D(var, kernel, stride):
    '''Full mode 3D convolution using stride view.

    Args:
        var (ndarray): 4d array to convolve along the last 3 dimensions.
            Shape of the array is (m, hi, wi, ci). Where m: number of records.
            hi, wi: height and width of input image. ci: channels of input image.
        kernel (ndarray): 4d filter to convolve with. Shape is (f1, f2, ci, co).
            where f1, f2: filter size. co: number of filters.
    Keyword Args:
        stride (int): stride along the mid 2 dimensions. Default to 1.
    Returns:
        conv (ndarray): convolution result.

    Note that the kernel is not filpped inside this function.
    '''
    if np.ndim(var) != 4:
        raise Exception("<var> dimension should be 4.")
    if np.ndim(kernel) != 4:
        raise Exception("<kernel> dimension should be 4.")
    stride = int(stride)
    m, hi, wi, ci = var.shape
    f1, f2, ci, co = kernel.shape

    # interleave 0s
    var2 = interLeave(var, stride-1, stride-1)
    # pad boundaries
    nout, pad_left, pad_right = compSize(hi, f1, stride)
    var2 = padArray(var2, pad_left, pad_right)
    # transpose kernel
    kernel = np.transpose(kernel, [0, 1, 3, 2])
    # convolve
    conv = conv3D3(var2, kernel, stride=1, pad=0)

    return conv

def interLeave(arr, sy, sx):
    '''Interleave array with rows/columns of 0s.

    Args:
        arr (ndarray): 4d array to interleave in the mid 2 dimensions.
        sy (int): number of rows to interleave.
        sx (int): number of columns to interleave.
    Returns:
        result (ndarray): input <arr> array interleaved with 0s.

    E.g.
        arr[0,:,:,0] = [[1, 2, 3],
                       [4, 5, 6],
                       [7, 8, 9]]
        interLeave(arr, 1, 2)[0,:,:,0] ->

        [[1, 0, 0, 2, 0, 0, 3],
         [0, 0, 0, 0, 0, 0, 0],
         [4, 0, 0, 5, 0, 0, 6],
         [0, 0, 0, 0, 0, 0, 0],
         [7, 0, 0, 8, 0, 0, 9]]
    '''

    m, hi, wi, ci = arr.shape
    shape = (m, hi+sy*(hi-1), wi+sx*(wi-1), ci)
    result = np.zeros(shape)
    result[:, 0::(sy+1), 0::(sx+1), :] = arr
    return result

def computeGradients(self, delta, act):
    '''Compute gradients of cost wrt filter weights

    Args:
        delta (ndarray): errors in filter ouputs.
        act (ndarray): activations fed into filter.
    Returns:
        grads (ndarray): gradients of filter weights.
        grads_bias (ndarray): 1d array, gradients of biases.

    The theoretical equation of gradients of filter weights is:

        \partial J / \partial W^{(l)} = a^{(l-1)} \bigotimes \delta^{(l)}

    where:
        J : cost function of network.
        W^{(l)} : weights in filter.
        a^{(l-1)} : activations fed into filter.
        \bigotimes : convolution in valid mode.
        \delta^{(l)} : errors in the outputs from the filter.
    '''
    grads = conv3Dgrad(act, delta)
    # gradient clip
    grads = np.clip(grads, -self.clipvalue, self.clipvalue)
    grads_bias = np.sum(delta, axis=(0, 1, 2))  # 1d

    return grads, grads_bias

def conv3Dgrad(act, delta):
    '''Compute gradients of convolution layer filters

    Args:
        act (ndarray): activation array as input to the filters. With shape
            (m, hi, wi, ci).  Where m: number of records.
            hi, wi: height and width of the input into the filters.
            ci: channels of input into the filters.
        delta (ndarray): error term as output from the filters. With shape
            (m, ho, wo, co): ho, wo: height and width of the output from the filters.
            co: number of filters in the convolution layer.
    Returns:
        conv (ndarray): gradients of filters, defined as:

            \partial J / \partial W^{(l)} = \sum[ a^{(l-1)} \bigotimes \delta^{(l)}]

        NOTE that the gradients are summed across the m records in <act> and
        <delta>.
    '''
    m, hi, wi, ci = act.shape
    m, ho, wo, co = delta.shape
    view = asStride(act, (ho, wo), stride=1)
    #conv = np.einsum('myxfgz,mfgo->yxzo', view, delta)
    conv = np.tensordot(view, delta, axes=([0, 3, 4], [0, 1, 2]))
    return conv

def backPropError(self, delta_in, z):
    '''Back-propagate errors

    Args:
        delta_in (ndarray): delta from the next layer in the network.
        z (ndarray): weighted sum of the current layer.
    Returns:
        result (ndarray): delta of the current layer.

    The theoretical equation for error back-propagation is:

        \delta^{(l)} = \delta^{(l+1)} \bigotimes_f Rot(W^{(l+1)}) \bigodot f'(z^{(l)})

    where:
        \delta^{(l)} : error of layer l, defined as \partial J / \partial z^{(l)}.
        \bigotimes_f : convolution in full mode.
        Rot() : is rotating the filter by 180 degrees, i.e. a kernel flip.
        W^{(l+1)} : weights of layer l+1.
        \bigodot : Hadamard (elementwise) product.
        f() : activation function of layer l.
        z^{(l)} : weighted sum in layer l.
    '''
    # filp kernel
    kernel_f = self.filters[::-1,::-1,:,:]
    result = fullConv3D(delta_in, kernel_f, stride=self.stride)
    result = result*dReLU(z)

    return result

\[
\delta^{(l-1)} = \sum_{k=1}^{n^{(l)}_c} [ \delta^{(l,k)} \otimes_f Rot_{180}(w^{(l,k)}) \odot g'(z^{(l-1)})]
\]

With the above, we can propagate the error from the end of a convolutional neural network to all the hidden layers.

Then the weights of the convolution filters can be computed using

\[
\frac{\partial J}{\partial w^{(l, k)}} = a^{(l-1)} \otimes
\delta^{(l,k)}, \; k=1,2,\cdots,n^{(l)}_c
\]

Then the convolution layer can be trained using, for instance, a gradient descent method.

Then numpy implementations are given, first for a serial version and then a vectorized version. These will be used in a later post when a complete CNN implementation is introduced.