The goal
This post covers the implementation of pooling layers in a
convolutional neural network using numpy. The complete code can be found in this Github repo file and file.
The pooling operation
Like convolution, the pooling operation also involves an input image (or input data cube), and a pooling kernel (or filter).
There are typically 2 types of pooling layers in a convolutional neural network:
- max-pooling: the maximum value in each pooling window is taken out as the pooling result. This is like grey-dilation in the image process field, or a maximum filtering. (see Figure 1 below for an illustration)
- average-pooling: the average value in each pooling window is taken out as the pooling result. This is like a moving average operation.
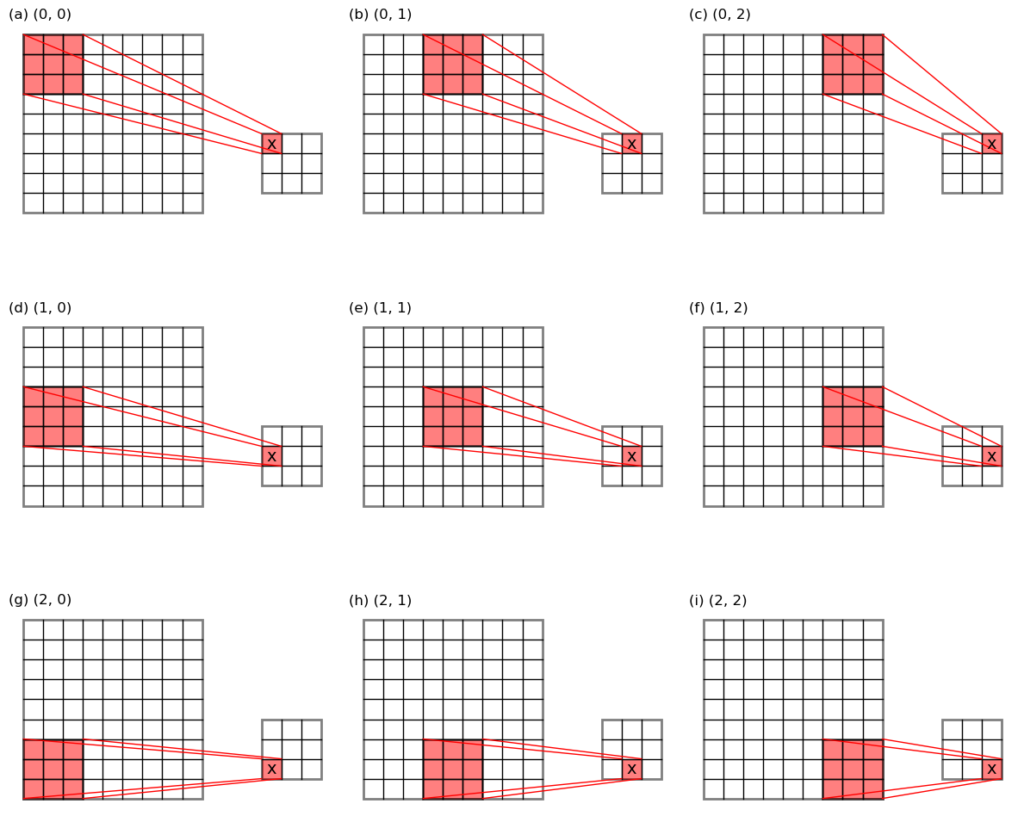

Like convolution, pooling is also parameterized by a stride. Suppose the input data have dimensions of \((h_i \times w_i \times c_i)\), where:
- \(h_i\), \(w_i\) being height and width,
- \(c_i\) being the depth.
The pooling kernel has a size of \((f \times f)\). Then with a stride of \(s\), the pooling result will have a size of \((h_o \times w_o \times c_o)\), where:
- \(h_o = [(h_i – f)/s] + 1\), the output height.
- \(w_o = [(w_i – f)/s] + 1\), the output width.
- \(c_o = c_i\), the output depth.
- \([ \, ]\) is the floor function
Note that padding is rarely used in pooling, therefore pooling results in a smaller sized output, and this is the point of doing pooling: to shrink the size of convolutional layers.
Also note that pooling does not alter the depth dimension. The max- or average- pooling happens independently in each channel, and the same number of channels are returned.
Numpy implementation of max- and average- pooling
Serial version
"Serial" here means that the pooling function handles 1 sample at a time. The input data are assumed to be either:
- 2D: with shape
(h, w). - 3D: with shape
(h, w, c).
where h, w are the image height/width, and c being the
depth/channel dimension.
def poolingOverlap(mat, f, stride=None, method='max', pad=False,
return_max_pos=False):
'''Overlapping pooling on 2D or 3D data.
Args:
mat (ndarray): input array to do pooling on the first 2 dimensions.
f (int): pooling kernel size.
Keyword Args:
stride (int or None): stride in row/column. If None, same as <f>,
i.e. non-overlapping pooling.
method (str): 'max for max-pooling,
'mean' for average-pooling.
pad (bool): pad <mat> or not. If true, pad <mat> at the end in
y-axis with (f-n%f) number of nans, if not evenly divisible,
similar for the x-axis.
return_max_pos (bool): whether to return an array recording the locations
of the maxima if <method>=='max'. This could be used to back-propagate
the errors in a network.
Returns:
result (ndarray): pooled array.
See also unpooling().
'''
m, n = mat.shape[:2]
if stride is None:
stride = f
_ceil = lambda x, y: x//y + 1
if pad:
ny = _ceil(m, stride)
nx = _ceil(n, stride)
size = ((ny-1)*stride+f, (nx-1)*stride+f) + mat.shape[2:]
mat_pad = np.full(size, 0)
mat_pad[:m, :n, ...] = mat
else:
mat_pad = mat[:(m-f)//stride*stride+f, :(n-f)//stride*stride+f, ...]
view = asStride(mat_pad, (f, f), stride)
if method == 'max':
result = np.nanmax(view, axis=(2, 3), keepdims=return_max_pos)
else:
result = np.nanmean(view, axis=(2, 3), keepdims=return_max_pos)
if return_max_pos:
pos = np.where(result == view, 1, 0)
result = np.squeeze(result)
return result, pos
else:
return result
Note that I’ve added the padding functionality just for good measure.
The function deals with either max- or average- pooling, specified by
the method keyword argument.
Also note that internally, it calls a asStride() function, which
was introduced in a previous post talking about 2d and 3d
convolutions. Without going into further details, the asStride()
trick takes out all the pooling windows (which in general will contain
overlapping grid cell locations, see the 9 red sub-matrices in Figure 1) in on go, allowing the max- or average- pooling to be carried out
in a single np.nanmax() or np.nanmean() function call.
The asStride() function is given below:
def asStride(arr, sub_shape, stride):
'''Get a strided sub-matrices view of an ndarray.
Args:
arr (ndarray): input array of rank 2 or 3, with shape (m1, n1) or (m1, n1, c).
sub_shape (tuple): window size: (m2, n2).
stride (int): stride of windows in both y- and x- dimensions.
Returns:
subs (view): strided window view.
See also skimage.util.shape.view_as_windows()
'''
s0, s1 = arr.strides[:2]
m1, n1 = arr.shape[:2]
m2, n2 = sub_shape[:2]
view_shape = (1+(m1-m2)//stride, 1+(n1-n2)//stride, m2, n2)+arr.shape[2:]
strides = (stride*s0, stride*s1, s0, s1)+arr.strides[2:]
subs = np.lib.stride_tricks.as_strided(
arr, view_shape, strides=strides, writeable=False)
return subs
Lastly, the return_max_pos keyword argument controls whether to
return the locations of the pooled maxima values in each pooling
window. This will be useful when training a convolutional neural
network during the backpropagation process.
An example
A toy example is given below illustrating the max-pooling process:
n = 6
f = 3
s = 3
np.random.seed(100)
mat = np.random.randint(0, 20, [n, n])
print('mat.shape:', mat.shape, 'filter size:', f, 'stride:', s)
print(mat)
po, pos = poolingOverlap(mat, f, stride=s, pad=False, return_max_pos=True)
print('Overlap pooling, no pad. Result shape:', po.shape)
print(po)
print('Max position pos.shape:')
print(pos.shape)
print('Max position in the (0,0) window:')
print(pos[0, 0])
print('Max position in the (0,1) window:')
print(pos[0, 1])
In this example, the data have shape (6, 6), filled with random
integers between 0 and 19.
The max pooling kernel is (3, 3), with a stride of 3
(non-overlapping). Therefore the output has a height/width of
[(6 - 3) / 3] + 1 = 2.
Meanwhile, the locations of the maxima values in each pooling window
are also recorded, and the returned value pos has a shape of (2, 2, 3, 3). The first 2 dimensions correspond to the row/column of the
pooled-out result, and the last 2 dimensions correspond to the pooling
window operating on that particularly location.
Output:
mat.shape: (6, 6) filter size: 3 stride: 3 [[ 8 3 7 15 16 10] [ 2 2 2 14 2 17] [16 15 4 11 16 9] [ 2 12 4 1 13 19] [ 4 4 3 7 17 15] [ 1 14 7 16 2 9]] Overlap pooling, no pad. Result shape: (2, 2) [[16 17] [14 19]] Max position pos.shape: (2, 2, 3, 3) Max position in the (0,0) window: [[0 0 0] [0 0 0] [1 0 0]] Max position in the (0,1) window: [[0 0 0] [0 0 1] [0 0 0]]
Vectorized version
The "vectorized" version is similar as the "serial" version, except that it handles multiple samples at a time, and the input data are assumed to be in the shape of:
(m, h, w, c)
where h/w/c being the image height/width/depth, as before. m
denotes the number of samples.
def poolingOverlap(mat, f, stride=None, method='max', pad=False,
return_max_pos=False):
'''Overlapping pooling on 4D data.
Args:
mat (ndarray): input array to do pooling on the mid 2 dimensions.
Shape of the array is (m, hi, wi, ci). Where m: number of records.
hi, wi: height and width of input image. ci: channels of input image.
f (int): pooling kernel size in row/column.
Keyword Args:
stride (int or None): stride in row/column. If None, same as <f>,
i.e. non-overlapping pooling.
method (str): 'max for max-pooling,
'mean' for average-pooling.
pad (bool): pad <mat> or not. If true, pad <mat> at the end in
y-axis with (f-n%f) number of nans, if not evenly divisible,
similar for the x-axis.
return_max_pos (bool): whether to return an array recording the locations
of the maxima if <method>=='max'. This could be used to back-propagate
the errors in a network.
Returns:
result (ndarray): pooled array.
See also unpooling().
'''
m, hi, wi, ci = mat.shape
if stride is None:
stride = f
_ceil = lambda x, y: x//y + 1
if pad:
ny = _ceil(hi, stride)
nx = _ceil(wi, stride)
size = (m, (ny-1)*stride+f, (nx-1)*stride+f, ci)
mat_pad = np.full(size, 0)
mat_pad[:, :hi, :wi, ...] = mat
else:
mat_pad = mat[:, :(hi-f)//stride*stride+f, :(wi-f)//stride*stride+f, ...]
view = asStride(mat_pad, (f, f), stride)
if method == 'max':
result = np.nanmax(view, axis=(3, 4), keepdims=return_max_pos)
else:
result = np.nanmean(view, axis=(3, 4), keepdims=return_max_pos)
if return_max_pos:
pos = np.where(result == view, 1, 0)
result = np.squeeze(result, axis=(3,4))
return result, pos
else:
return result
Similarly, the asStride() function is also a bit different from the
"serial" version, but the general idea is the same. The function is
given below:
def asStride(arr, sub_shape, stride):
'''Get a strided sub-matrices view of an ndarray.
Args:
arr (ndarray): input array of rank 4, with shape (m, hi, wi, ci).
sub_shape (tuple): window size: (f1, f2).
stride (int): stride of windows in both 2nd and 3rd dimensions.
Returns:
subs (view): strided window view.
This is used to facilitate a vectorized 3d convolution.
The input array <arr> has shape (m, hi, wi, ci), and is transformed
to a strided view with shape (m, ho, wo, f, f, ci). where:
m: number of records.
hi, wi: height and width of input image.
ci: channels of input image.
f: kernel size.
The convolution kernel has shape (f, f, ci, co).
Then the vectorized 3d convolution can be achieved using either an einsum()
or a tensordot():
conv = np.einsum('myxfgc,fgcz->myxz', arr_view, kernel)
conv = np.tensordot(arr_view, kernel, axes=([3, 4, 5], [0, 1, 2]))
See also skimage.util.shape.view_as_windows()
'''
sm, sh, sw, sc = arr.strides
m, hi, wi, ci = arr.shape
f1, f2 = sub_shape
view_shape = (m, 1+(hi-f1)//stride, 1+(wi-f2)//stride, f1, f2, ci)
strides = (sm, stride*sh, stride*sw, sh, sw, sc)
subs = np.lib.stride_tricks.as_strided(
arr, view_shape, strides=strides, writeable=False)
return subs
The unpooling operation
Unpooling is like the inverse of pooling, and is used during the backpropagation stage of the training process of a convolutional neural network.
For max-pooling, unpooling puts the input error values back to the original locations where the maxima values have been pooled out, and fills the rest of the places with 0s. This is why we need to keep a record of the maximum value locations during the pooling stage. See the schematic below for an illustration.
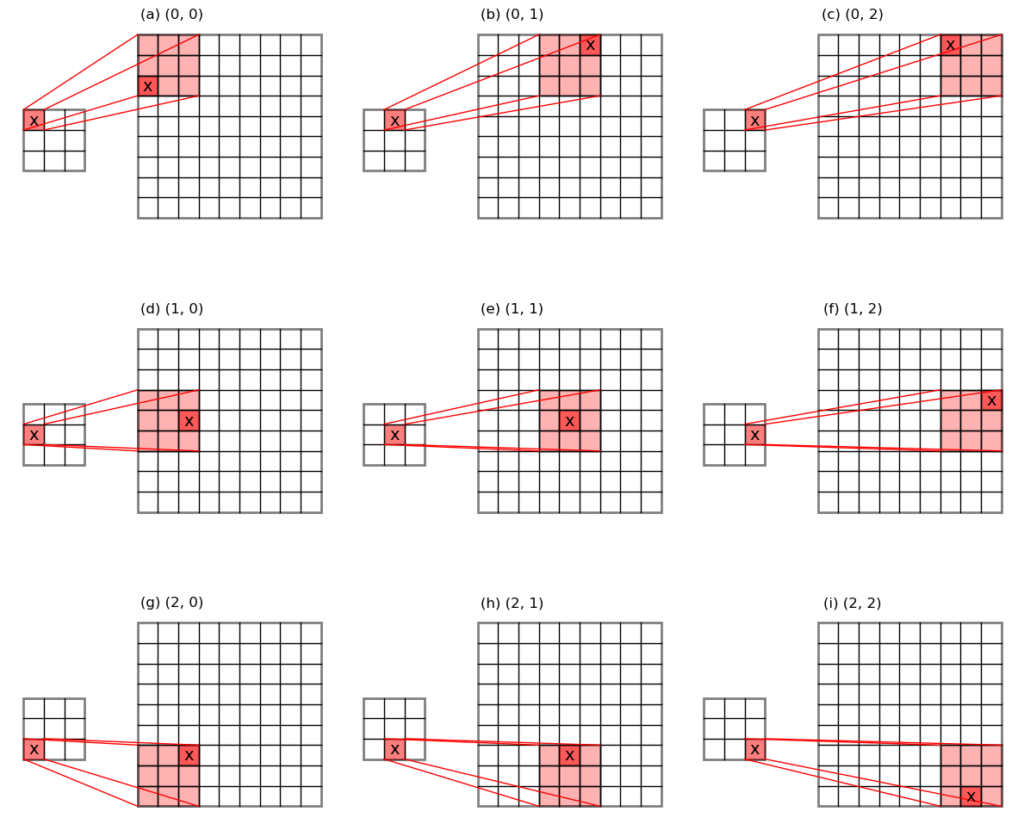

For average-pooling, unpooling divides the input error values evenly across the pooling window, and puts them back to their original places.
Numpy implementation of max-unpooling
We would attack the unpooling problem separately for max- and average- pooling. This section introduces the "serial" and "vectorized" implementations of max-unpooling.
For max-pooling, aside from the input array (mat) to unpool, it also
requires:
- the array recording the maxima value locations:
pos, - the shape of the array to unpool to:
ori_shape, - the stride used during the pooling stage:
stride.
Serial version
Corresponding to the serial version of the pooling function, serial
version of max-unpooling assumes that the input (mat) is either 2D or 3D:
For 2D input: mat is the max-pooled 2D data. The pos
argument has a shape of (iy, ix, cy, cx) where iy, ix give the
row/column sizes of the max-pooled array,
cy, cx is the same as the max-pooling kernel/filter.
For instance, using the example given above, the top-left-most number
in the max-pooled array is 16:
[[16 17]
[14 19]]
therefore, iy = 0 and ix = 0 for the top-left-most number 16.
This number was taken from this 3 x 3 sub-array from the original
array:
[[ 8 3 7 ]
[ 2 2 2 ]
[16 15 4 ]]
In this particularly case, the maximum value 16 occurs at location
(2, 0) inside the pooling window, therefore the sub-array of pos(0,0)
has a value of 1 at (2, 0) correspondingly:
[[0 0 0]
[0 0 0]
[1 0 0]]
After unpooling, the input error value (denoted as x) will be put to location of the 1, in the top-left most 3 x 3 sub-array:
[[ 0 0 0 0 0 0]
[ 0 0 0 0 0 0]
[ x 0 0 0 0 0]
[ 0 0 0 0 0 0]
[ 0 0 0 0 0 0]
[ 0 0 0 0 0 0]]
After putting backing all input error values, the unpooled array will
have error values located at these locations, denoted as x:
[[ 0 0 0 0 0 0]
[ 0 0 0 0 0 x]
[ x 0 0 0 0 0]
[ 0 0 0 0 0 x]
[ 0 0 0 0 0 0]
[ 0 x 0 0 0 0]]
For 3D input of mat: mat is the max-pooled 3D data. The pos
has shape (iy, ix, cy, cx, cc), the extra cc dimension is the
depth dimension.
The function is given below:
def unpooling(mat, pos, ori_shape, stride):
'''Undo a max-pooling of a 2d or 3d array to a larger size
Args:
mat (ndarray): 2d or 3d array to unpool on the first 2 dimensions.
pos (ndarray): array recording the locations of maxima in the original
array. If <mat> is 2d, <pos> is 4d with shape (iy, ix, cy, cx).
Where iy/ix are the numbers of rows/columns in <mat>,
cy/cx are the sizes of the each pooling window.
If <mat> is 3d, <pos> is 5d with shape (iy, ix, cy, cx, cc).
Where cc is the number of channels in <mat>.
ori_shape (tuple): original shape to unpool to.
stride (int): stride used during the pooling process.
Returns:
result (ndarray): <mat> unpoolled to shape <ori_shape>.
'''
assert np.ndim(pos) in [4, 5], '<pos> should be rank 4 or 5.'
result = np.zeros(ori_shape)
if np.ndim(pos) == 5:
iy, ix, cy, cx, cc = np.where(pos == 1)
iy2 = iy*stride
ix2 = ix*stride
iy2 = iy2+cy
ix2 = ix2+cx
values = mat[iy, ix, cc].flatten()
result[iy2, ix2, cc] = values
else:
iy, ix, cy, cx = np.where(pos == 1)
iy2 = iy*stride
ix2 = ix*stride
iy2 = iy2+cy
ix2 = ix2+cx
values = mat[iy, ix].flatten()
result[iy2, ix2] = values
return result
An example
Following up the above example, let’s unpool the max-pooled array of
[[16 17]
[14 19]]
unpo = unpooling(po, pos, mat.shape, s)
print('Unpooling result shape:', unpo.shape)
print(unpo)
The output:
Unpooling result shape: (6, 6) [[ 0. 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 0. 17.] [16. 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 0. 19.] [ 0. 0. 0. 0. 0. 0.] [ 0. 14. 0. 0. 0. 0.]]
It can be seen that the unpooling process reverts back to the original
shape of (6, 6), and the maxima values are put back to their
original locations.
Vectorized version
The "vectorized" version looks similar as the "serial" version, except
that we are assuming the input array mat to be 4D: (m, h, w, c),
where:
msample size,h, wimage height/width,cimage depth.
It is also assumed that mat has been
max-pooled from a 4D data array (see the "vectorized" poolingOverlap()
function above). Correspondingly, the maxima value positions recorded
in pos is 6D: (m, iy, ix, cy, cx, cc), where:
m: sample size, as above,iy, ix: size of the max-pooled array,cy, cx: max-pooling kernel size,cc: depth dimension size.
The function definition is given below:
def unpooling(mat, pos, ori_shape, stride):
'''Undo a max-pooling of a 4d array to a larger size
Args:
mat (ndarray): 4d array to unpool on the mid 2 dimensions.
pos (ndarray): array recording the locations of maxima in the original
array. If <mat> is 4d, <pos> is 6d with shape (m, h, w, y, x, c).
Where h/w are the numbers of rows/columns in <mat>,
y/x are the sizes of the each pooling window.
c is the number of channels in <mat>.
ori_shape (tuple): original shape to unpool to: (m, h2, w2, c).
stride (int): stride used during the pooling process.
Returns:
result (ndarray): <mat> unpoolled to shape <ori_shape>.
'''
assert np.ndim(pos)==6, '<pos> should be rank 6.'
result = np.zeros(ori_shape)
im, ih, iw, iy, ix, ic = np.where(pos == 1)
ih2 = ih*stride
iw2 = iw*stride
ih2 = ih2+iy
iw2 = iw2+ix
values = mat[im, ih, iw, ic].flatten()
result[im, ih2, iw2, ic] = values
return result
Numpy implementation of average-unpooling
The unpooling of average-pooled array works quite differently as the unpooling of max-pooling, because we do not need to put the error values to some specific locations, but only need to send the evenly divided errors back to their original pooling window locations. See Figure 3 below for an illustration.
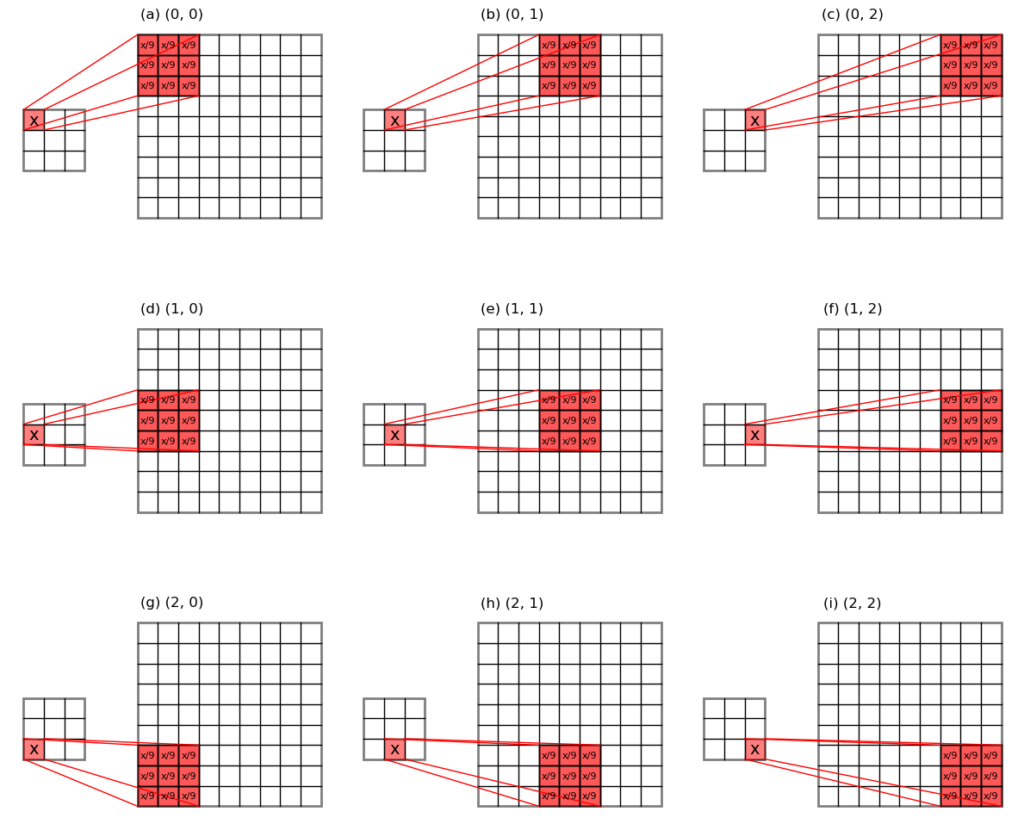

It works by firstly working out the evenly divided error, and duplicating that mean error a number of times. Both can be achieved by knowing the pooling kernel size. Then rest of the game is just some housing keeping to make sure the dimensions are correct.
Serial version
Again, "serial" version handles one input sample at a time, and the
mat array is assumed to be 2D or 3D ((h, w) or (h, w, c).
The function is given below:
def unpoolingAvg(mat, f, ori_shape):
'''Undo an average-pooling of a 2d or 3d array to a larger size
Args:
mat (ndarray): 2d or 3d array to unpool on the first 2 dimensions.
f (int): pooling kernel size.
ori_shape (tuple): original shape to unpool to.
Returns:
result (ndarray): <mat> unpoolled to shape <ori_shape>.
'''
m, n = ori_shape[:2]
ny = m//f
nx = n//f
tmp = np.reshape(mat, (ny, 1, nx, 1)+mat.shape[2:])
tmp = np.repeat(tmp, f, axis=1)
tmp = np.repeat(tmp, f, axis=3)
tmp = np.reshape(tmp, (ny*f, nx*f)+mat.shape[2:])
result=np.zeros(ori_shape)
result[:tmp.shape[0], :tmp.shape[1], ...]= tmp
return result
Vectorized version
Again, "vectorized" version handles m samples at a time. The input
mat is assumed to be 4D: (m, h, w, c).
Function given below:
def unpoolingAvg(mat, f, ori_shape):
'''Undo an average-pooling of a 4d array to a larger size
Args:
mat (ndarray): input array to do unpooling on the mid 2 dimensions.
Shape of the array is (m, hi, wi, ci). Where m: number of records.
hi, wi: height and width of input image. ci: channels of input image.
f (int): pooling kernel size in row/column.
ori_shape (tuple): original shape to unpool to: (m, h2, w2, c).
Returns:
result (ndarray): <mat> unpoolled to shape <ori_shape>.
'''
m, hi, wi, ci = ori_shape
ny = hi//f
nx = wi//f
tmp = np.reshape(mat, (m, ny, 1, nx, 1, ci))
tmp = np.repeat(tmp, f, axis=2)
tmp = np.repeat(tmp, f, axis=4)
tmp = np.reshape(tmp, (m, ny*f, nx*f, ci))
result=np.zeros(ori_shape)
result[:, :tmp.shape[1], :tmp.shape[2], :] = tmp
return result
Summary
Max- or average- pooling works on individual image channels independently, and both shrinks the data size in height/width dimensions.
Unpooling does the inverse and "broadcasts" a smaller sized image to a larger array.
In the max-unpooling process, the recorded position information is used to send back the errors to the locations of the maxima values during the max-pooling process. The rest of the array space is filled with 0s.
In the average-unpooling process, the input errors are evenly divided into a pooling window, and sent back to the original locations.
For max- and average- pooling and unpooling, we developed a "serial"
version and a "vectorized" version using numpy. The "vectorized"
version has the advantage of being able to handle multiple samples at
a time, and can considerably speed up the training process of a
convolutional neural network.



[…] Pytorch使用第一个最大值出现的地方,而一些来源使用另一种方法(他使用pos = np.where(result == view, 1, 0),这本质上是为所有最大值出现的地方记录1)。 […]